 |
|
|
[Sponsors] | |||||
|
|
|
#101 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#102 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#103 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#104 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Stable but not oscillation-free. PS: writing your equations, you have to use a different notation for the time derivative, it is not a partial derivative. In lagrangian formulation you are integrating the equation from t to t+dt but not at a fixed position. |
||
|
|

|
||
|
|
|
#105 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Yes, that's correct, but you integrate it in fixed mass.
|
|
|
|

|
|
|
|
|
#106 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#107 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
So in Eulerian formulation you end up with linearized discrete equations with an advective term and diffusion term + any other sources.
With a lagrangian formulation you don't have an "advective" term but now you have a non-linear Laplacian term which looks like a diffusion term but which contains the equivalent physics the as the advection + diffusion term if done the Eulerian way. It not really correct to call it a "diffusion" term because it does contain advective physics in it (they are just hiding in the non-linearities). All else being equal, the stability constraints from the Eulerian way will transfer directly over to the Lagrangian formulation. In general, the advection term and diffusion term in an Eulerian solver would have different discretization schemes. Your Lagrangian solver is a distinct case because you have only one term to formally discretize so you do not get to pick and choose schemes exactly the same way. Nonetheless, that doesn't mean that your superdooperawesome Lagrangian way will be any more stable because all those linear instabilities are now transferred to the non-linearities in your scheme. Still, for low Peclet numbers your Lagrangian way could still provide some benefit since here it does make sense to central difference both the advective and diffusive terms. At the end of it all, there might be some convenience gained as you originally hoped. |
|
|
|

|
|
|
|
|
#108 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Now I have just done an explicit scheme, I was thinking of doing an implicit scheme, using the weighted-average method. So would I use something like:
![\frac{u_{i+1,j}-u_{i,j}}{\delta t}=\theta\left[F_{i+1}\right]_{j-\frac{1}{2}}^{j+\frac{1}{2}}+(1-\theta)\left[F_{i}\right]_{j-\frac{1}{2}}^{j+\frac{1}{2}} \frac{u_{i+1,j}-u_{i,j}}{\delta t}=\theta\left[F_{i+1}\right]_{j-\frac{1}{2}}^{j+\frac{1}{2}}+(1-\theta)\left[F_{i}\right]_{j-\frac{1}{2}}^{j+\frac{1}{2}}](/Forums/vbLatex/img/230e14429921cb2b75f856f805d848bd-1.gif) If this is okay, my plan was to do a Fourier analysis to find a value of theta that gives the best value for convergence for delta t. I've only seen this sort of analysis done for a single equation rather than a system. |
|
|
|

|
|
|
|
|
#109 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#110 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Your problem is non linear since F=F(u), the Fourier analysis for the linear case is well known in literature but gives only some infos you have then to consider as an indication for the non linear problem. I suggest to use the CN scheme (theta=1/2) and a linearization to work with the linear algebric tridiagonal system. This way you can use the Thomas algorithm. |
|
|
|

|
|
|
|
|
#111 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
If what you are concerned with is stability then there is no question.Theta = 0 is for sure the most stable. The reason for optimizing theta is to obtain higher accuracy (at the expense of stability).
|
|
|
|

|
|
|
|
|
#112 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I was reading the book, whose link you sent, and they derived a value of theta that allowed dt to be of the same order of dx. Obviously that allows for a huge speedup in the code. I was wondering if I might be able to do the same thing.
I can code up CN method easily now I have a the fluxes, and I can combine that with the Newton- Raphson method to get the solution. I could linearise around the initial condition I suppose. |
|
|
|

|
|
|
|
|
#113 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
So I coded up the implicit method and I am using the Newton-Raphson to solve the resulting algebraic equations. The problem comes in when I am computing the Jacobian and getting the next iteration.
The specific volume equation is causing issues: ![\frac{\nu_{i+1,j}-u_{i,j}}{\delta t}-\theta[u]_{i+1,j-\frac{1}{2}}^{i+1,j+\frac{1}{2}}-(1-\theta)[u]_{i,j-\frac{1}{2}}^{i,j+\frac{1}{2}}=f_{j}=0 \frac{\nu_{i+1,j}-u_{i,j}}{\delta t}-\theta[u]_{i+1,j-\frac{1}{2}}^{i+1,j+\frac{1}{2}}-(1-\theta)[u]_{i,j-\frac{1}{2}}^{i,j+\frac{1}{2}}=f_{j}=0](/Forums/vbLatex/img/894669e0ed8f51c12a3265f42aeba033-1.gif) These are a set of algebraic equations in the required variables. When I compute the Jacobian I get something like: 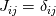 when 1<=i,j<=N So when I compute the next iteration I use the following equation: 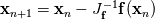 I'm getting my update as a really small value. I'm not too sure what is going on. My code is: Code:
clear;clc;
c_p=1;
global N
N=200;
M=10^5;
x=linspace(0,1,N+1);
t=linspace(0,20,M);
L=zeros(M,1);
global dt
dt=t(2);
dx=x(2);
nu=zeros(M,N);
u=zeros(M,N);
X=zeros(M,N+1);
X(1,:)=x;
rho_half(1:N)=0.6;
y_0(N+1:2*N)=0;
y_old=zeros(1,2*N);
nu(1,:)=1./rho_half;
y_old(1:N)=nu(1,:);
v(1,:)=y_0(N+1:2*N);
theta=0.5;
rho_0=zeros(1,N+1);
rho_0(2:N)=0.5*(rho_half(1,N-1)+rho_half(2:N));
rho_0(1)=1.5*rho_half(1)-0.5*rho_half(2);
rho_0(N+1)=1.5*rho_half(N)-0.5*rho_half(N-1);
h=cumtrapz(x,rho_0);
global nu_m
nu_m(1:N)=1;
global dh
dh=diff(h);
tol=1e-7;
global eta_0
eta_0=0.0025;
r=eta_0*dt/max(dh)^2;
for i=2:M
y_init=1.001*y_old;
y = Newton(tol,y_old,y_init,theta);
nu(i,:)=y(1:N);
u(i,:)=y(N+1:2*N);
%Compute the new grid
X(i,2:N)=X(i-1,2:N)+0.5*dt*(u(i,1:N-1)+u(i,2:N));
dum=dt*(1.5*u(i,N)-0.5*u(i,N-1));
X(i,N+1)=X(i-1,N+1)+dt*(1.5*u(i,N)-0.5*u(i,N-1));
L(i)=X(i,N+1);
if L(i)<0
flag=0;
disp('Length of piece is less than zero');
return;
end
y_old=y;
end
function y=mass_flux(nu,u)
global N
global dh
y=zeros(1,N+1);
y(2:N)=0.5*(u(2:N)+u(1,N-1));
y(N+1)=u(N)-0.25*dh(N)*(3*nu(N)-nu(N-1));
end
function y=flux(u,nu,nu_0)
global N
global dh
y=zeros(1,N+1);
nu_face=0.5*(nu(1:N-1)+nu(2:N));
y(2:N)=(4*zeta(nu_face,nu_0(2:N))./nu_face).*((u(2:N)-u(1:N-1))./(dh(2:N)+dh(1:N-1)));
nu_L=1.5*nu(1)-0.5*nu(1);
nu_0_L=1.5*nu_0(1)-0.5*nu_0(1);
y(1)=(zeta(nu_L,nu_0_L)/nu_L)*(2*u(1)/dh(1));
y(N+1)=-zeta(1.5*nu(N)-0.5*nu(N-1),1.5*nu_0(N)-0.5*nu_0(N-1));
end
function y=zeta(z,nu_0)
global eta_0
x=1-nu_0./z;
y = 2*(1-x).^3*eta_0./(3*x);
end
function [J] = jacobian(y_old,y,theta)
% Computes the Jacobian matrix of the function f(x)
% f: function handle that returns a vector of function values
% x: column vector of independent variables
% Number of function values and independent variables
n = length(y); % number of independent variables
% Initialize Jacobian matrix
eps=1e-5; % could be made better
J = zeros(n,n);
T=zeros(1,n);
for i=1:n
T(i)=1;
fPlus = sintering_RHS(y_old,y+eps*T,theta);
fMinus = sintering_RHS(y_old,y-eps*T,theta);
J(:,i) = (fPlus-fMinus)/(2*eps);
T(i)=0;
end
end
function f=sintering_RHS(y_0,y,theta)
global nu_m
N=floor(length(y)/2);
f=zeros(1,2*N);
f_mass=mass_flux(y(1:N),y(N+1:2*N));
f_mass_0=mass_flux(y_0(1:N),y_0(N+1:2*N));
f_mom=flux(y(N+1:2*N),y(1:N),nu_m);
f_mom_0=flux(y_0(N+1:2*N),y_0(1:N),nu_m);
global dt
f(1:N)=y(1:N)-y_0(1:N)-dt*theta*(f_mass(2:N+1)-f_mass(1:N))-(1-theta)*dt*(f_mass_0(2:N+1)-f_mass(1:N));
f(N+1:2*N)=y(N+1:2*N)-y_0(N+1:2*N)-dt*theta*(f_mom(2:N+1)-f_mom(1:N))-(1-theta)*dt*(f_mom_0(2:N+1)-f_mom_0(1:N));
end
function [y] = Newton(tol,y_old,y0,theta)
iter = 0;
maxiter = 100;
error=10;
while (error > tol) && (iter < maxiter)
J0 = jacobian(y_old,y0,theta);
delta_y = -J0\y0';
y = y0 + delta_y';
error=norm(sintering_RHS(y0,y,theta));
y0 = y;
iter = iter + 1;
fprintf('Iteration %i, norm = %.2f\n', iter, error)
end
end
|
|
|
|

|
|
|
|
|
#114 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Could you explicitly write the equation ? |
||
|
|

|
||
|
|
|
#115 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#116 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Considering your pdf file, are you solving only Eq.(18)? What about (19)?
In the equation you wrote, you have the LHS where the unknowns are ni(i+1) and u(i+1), the rest of the equations is known and represent the RHS. In this form, it does not seem a non-linear equation but a linear equation that needs a second equation for u to be closed. Otherwise, to be closed you have to introduce some functional relation ni=f(u). For this reason I asked you to write the full method. |
|
|
|

|
|
|
|
|
#117 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
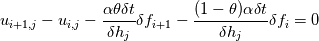 Where: 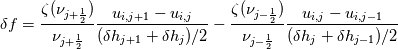 The issue seems to be the Jacobian though. |
||
|
|

|
||
|
|
|
#118 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
If you substitute ui+1 in the previous one (mass), you get a single non-linear equation in the form A(ni).nij+1 =known term here you can introduce a linearization for A. Are you doing this way? |
|
|
|

|
|
|
|
|
#119 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
No, I'm solving the set of non-linear equations using the Newton-Raphson method.
|
|
|
|

|
|
|
|
|
#120 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| multiphaseEulerFoam FOAM FATAL IO ERROR | qutadah.r | OpenFOAM Running, Solving & CFD | 11 | December 10, 2021 21:18 |
| SU2 7.0.7 Built on CentOS 7, parallel computation pyscript mpi exit error? | EternalSeekerX | SU2 | 3 | October 9, 2020 19:28 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| Gradient evaluation in Finite Volume Methods | yidongxia | Main CFD Forum | 7 | August 6, 2012 11:23 |
| Unstructured grid finite volume methods | Marcus | Main CFD Forum | 3 | December 5, 2000 01:25 |