 |
|
|
[Sponsors] | |||||
|
|
|
#81 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
What you have is not a BC. You are not constraining u. You are just asking what is u on the boundary and this is flux interpolation/reconstruction the same as any other face flux. Just because it is a boundary value does not mean it is a boundary condition. For example, you also calculate many higher order derivatives d^n u / dh^n on a boundary or even du/dt on a boundary, but none of them are boundary conditions since they are not constraints.
The boundary condition at the end of the rod is du/dh and that is exactly what Filippo has done. If you want to change your boundary condition to a Robin type, then it would obviously be u + du/dh = something instead of du/dh=something. But you said you have a Neumann condition at the end. |
|
|
|

|
|
|
|
|
#82 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
u1(N+1)=u1(N)-1*(dx) |
|
|
|

|
|
|
|
|
#83 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#84 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
What I am not sure to understand is the congruence between d ni/dt = du/dh as equation and du/dh= -ni(t) at the boundary. However, assuming i_max the node on the right boundary and n the time level, you can also write a second order accurate boundary condition by using du/dh|i_max=(3*u(i_max,n)-4*u(i_max-1,n)+u(i-max-2))/(2*h) so that u(i_max,n)=2*h*(-ni(i_max,n)) +4*u(i_max-1,n)-3*u(i_max,n) of course, h is assumed to be constant. |
||
|
|

|
||
|
|
|
#85 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#86 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#87 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
The non-constant h is like the non-constant x in Eulerian solvers. You are no longer guaranteed formally second order accuracy all the time but you can tune the 3 4 1 stencil such that it is more second order. And then you get into flux limiters and what not. Since you are so mathematically inclined it should be no issue for you to accept that there exists a stencil that gives you exactly the properties that you want. But it illustrates the key concept of how you would discretize it.
|
|
|
|

|
|
|
|
|
#88 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
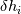 remains the same value for all time and only depends upon the initial density configuration. remains the same value for all time and only depends upon the initial density configuration. Can I combine the FV method with things like Backward Euler to get a larger timestep? My dt is currently tiny. |
||
|
|

|
||
|
|
|
#89 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Just define a second degree polynomial along h(i_max,n), h(i_max-1,n), h(i_max-2,n) and express the derivative at i_max. |
||
|
|

|
||
|
|
|
#90 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The numerical stability constraint depends not only by type of scheme but on the physical parameters and the mesh size. You need to evaluate the time step constrained by |u*dt/h|max<1 |D*dt/h^2|max<0.5 for an explicit first order scheme. |
||
|
|

|
||
|
|
|
#91 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
I just need to increase the timestep somehow. Can I combine methods? Like a 2-step Euler or something? |
||
|
|

|
||
|
|
|
#92 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
There is a tradeoff. Backward Euler means each time you must solve a system of equations and this is what we call implicit time-stepping. It tolerates larger dt (you can probably easily squeeze out 10x larger dt) but the solve time is longer per step by also an order of magnitude since marching Aa=a' forward in time is very fast whereas solving B*b'=b is very slow. Unless you need a stable code valid over a wide range of conditions it is not strictly necessary nor beneficial to go the implicit route. Also keep in mind, stability doesn't mean oscillation free either.
Ultimately your dt size is determined by your non-dimensional BCs and non-dimensional time you want to integrate over. The easiest way to increase the allowable size of dt is to use a coarser grid. But you might say ohhh but I want good resolution in h. Well then, you know it isn't free. |
|
|
|

|
|
|
|
|
#93 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
My initial attempt was to use the implicit method, as it's good to do and can get nice solutions in reasonably fast times. I've been reading the book on numerical methods I was recommended and I think I need to do some stability analysis to find the best scheme out there. My initial question was can I combine this with the FVM? It's become a fast favourite this past week or so. |
||
|
|

|
||
|
|
|
#94 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The implicit CN scheme is largely used for the diffusive terms. However, I suspect that in your specific problem, owing to your coupling with ni and h, you get a non-linear algebric system. On the other hand, be aware that using large time-step you get also a lower time accuracy. Think about the physical constraint, does your problem requires to describe accurately the transient? |
||
|
|

|
||
|
|
|
#95 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
I'm interested in how quickly my rod shrinks and the density distribution as time progresses. The BC on the right deals with that, but I scaled it out, and it's only in one constant now. I think that this makes things cleaner, and the numerics easier. |
||
|
|

|
||
|
|
|
#96 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I am used to consider large 3d and unsteady problems where you really need of performances and efficiency of the code. Try the CN method for the diffusion, check if you really get a valid improvement. |
||
|
|

|
||
|
|
|
#97 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#98 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
You have to consider that if your problem is mainly of convective type, the implicit part of the diffusive terms will not solve all your requirements, the CFL will be dominant. |
||
|
|

|
||
|
|
|
#99 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Yes backward Euler is compatible with FVM. Implicit time-stepping is one of the most popular implementations in commercial FVM codes.
1st order Backward Euler is the hello world equivalent for implicit time stepping. 2nd order backward Euler is usually the next scheme implemented in a dev code. Crank Nicolson in time is a personal favorite of mine. Note that the classical 0 1 stencil is generally unstable for advective problems due to non-linearities and a 0 0.9 or less stencil is often used for practical problems. If you want to learn implicit time-stepping I encourage you to start with the backward Euler case, any other temporal schemes is just a change in stencil just like changing spatial schemes. Fully implement the backward Euler case so you can actually see the "linear system" I was referring to some months back. |
|
|
|

|
|
|
|
|
#100 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
As the co-ordinates I've used makes the convective term dissappear, the only term that appears is the diffusion term right?
|
|
|
|

|
|
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| multiphaseEulerFoam FOAM FATAL IO ERROR | qutadah.r | OpenFOAM Running, Solving & CFD | 11 | December 10, 2021 21:18 |
| SU2 7.0.7 Built on CentOS 7, parallel computation pyscript mpi exit error? | EternalSeekerX | SU2 | 3 | October 9, 2020 19:28 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| Gradient evaluation in Finite Volume Methods | yidongxia | Main CFD Forum | 7 | August 6, 2012 11:23 |
| Unstructured grid finite volume methods | Marcus | Main CFD Forum | 3 | December 5, 2000 01:25 |