 |
|
|
[Sponsors] | |||||
|
|
|
#61 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Ho do you express nu as a function of u? That seems more a sort of Robin condition, not exactly Neumann.
|
|
|
|

|
|
|
|
|
#62 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
In order to get an idea of the Reynolds number Vr*L/D, one needs to estimate Vr from the BCs:
du/dx=-k*nu -> du*/dx*=-k*nu*L/Vr Thus, since this is the driving force, one prescribe Vr=k*nu*L and Re= k*nu*L^2/D But that assumes nu=constant, but if you have nu(u) the issue is different. |
|
|
|

|
|
|
|
|
#63 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#64 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#65 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Your M-files shows a solution not only oscillating but under instability, the values are aroud 10^73. Thus, a bug in the code or the numerical stability constraints are not satisfied. |
||
|
|

|
||
|
|
|
#66 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
A further big issue is that you have simply assigned
t=linspace(0,3,M); x=linspace(0,1,N+1); dt=t(2); dx=x(2); without any check about the CFDL and diffusive stability constraint |
|
|
|

|
|
|
|
|
#67 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
%Eulerian code for viscous Burgers equation with Neumann BC at x_max
clear;clc; N=200; %This is the number of point in the x-variable, and also h. M=1000; %This is the discretisation for the time variable; t=linspace(0,0.0003,M); x=linspace(0,1,N+1); nu=0.1; u=zeros(M,N+1); %This is the velocity; dt=t(2); dx=x(2); D=0.01; k=-0.1; Re=1.0; % initial condition for u M=1 u0(1:N+1)=0.0 ; %BC u0(1)=0 ; u0(N+1)=u0(N)-1 ; u(M,1:N+1)=u0 ; for k=1:1000, % fluxes for i=2:N+1, conv=0.5*(u0(i)^2+u0(i-1)^2)/2.; diff=(u0(i)-u0(i-1))/dx/Re; f(i)=-conv+diff; end % Update for i=2:N, u1(i)=u0(i)+dt*(f(i+1)-f(i))/dx; end %BC u1(1)=0; u1(N+1)=u1(N)-1; %Swap u0(1:N+1)=u1(1:N+1); u(k+1,1:N+1)=u1(1:N+1); plot(u1) end pause contour(u) end |
|
|
|

|
|
|
|
|
#68 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Se the few-lines code for solving the Burgers equation in FV formulation on a Eulerian grid.
Again, you have to compute the time step allowing the stability. |
|
|
|

|
|
|
|
|
#69 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
||
|
|

|
|
|
|
|
#70 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
In my code I used a very small time step as you can see. Try running. |
||
|
|

|
||
|
|
|
#71 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
So I do a von Neumann stability analysis on the equations: 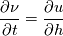 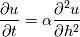 and find out the requirements for stability and try that? |
||
|
|

|
||
|
|
|
#72 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
For the stability analysis you have to work on the numerical schemes not on the linear PDEs. Choose a scheme and the do that. |
||
|
|

|
||
|
|
|
#73 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
Thank you for extending my knowledge of finite volume methods and also getting my code working. |
||
|
|

|
||
|
|
|
#74 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
So now I've got it working with the Euler method, are there any other methods I can use that will allow me to decrease the timestep?
|
|
|
|

|
|
|
|
|
#75 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
For example, here you can read a lot of topics about numerical solution of PDEs http://www.math.science.cmu.ac.th/do...20of%20PDE.pdf |
||
|
|

|
||
|
|
|
#76 | |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#77 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
That is as same as happens in turbulence for eddy viscosity model. You have to compute D on any single face of the volumes by introducing the functional relation D=f(x,t). |
||
|
|

|
||
|
|
|
#78 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
A scaled version of the equations are:
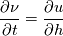 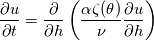 Where 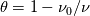 is the porosity, and the function is defined as is the porosity, and the function is defined as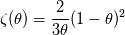 The boundary conditions are given as: 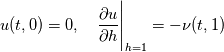 The code is playing up, and I was thinking it was something to do with the speed at which the diffusion happens, the speed seems to be increasing negatively quicker than the density seems to be increasing which I find odd. Another thing I was thinking about is using the Neuman BC for u, to give me a BC for u at h=1, by writing the derivative as a one-sided stencil to get a value for u(t,1). Thoughts? Do you think that will things better? |
|
|
|

|
|
|
|
|
#79 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The Neumann Bc at x=xmax is what I used in the code I posted. |
|
|
|

|
|
|
|
|
#80 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I've been looking at your code, and I'm not sure what you've done. I don't quite understand how you've applied the BC. You've solved the viscous burgers equation, I am looking at a system, my conservation of mass, in terms of the finite volume approach is
![\int_{h_{j}-\frac{\delta h}{2}}^{h_{j}+\frac{\delta h}{2}}\frac{\partial \nu}{\partial t}dh=\left[ u\right]_{h_{j}-\frac{\delta h}{2}}^{h_{j}+\frac{\delta h}{2}} \int_{h_{j}-\frac{\delta h}{2}}^{h_{j}+\frac{\delta h}{2}}\frac{\partial \nu}{\partial t}dh=\left[ u\right]_{h_{j}-\frac{\delta h}{2}}^{h_{j}+\frac{\delta h}{2}}](/Forums/vbLatex/img/0969633941d1c1838b4b5b37ac4631b9-1.gif) So on the end, I need to find an expression for 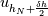 I think that If you use a one-sided backward derivative, you can use it to obtain it to get u on the right boundary. |
|
|
|

|
|
 |
| Tags |
| finite volume method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| multiphaseEulerFoam FOAM FATAL IO ERROR | qutadah.r | OpenFOAM Running, Solving & CFD | 11 | December 10, 2021 21:18 |
| SU2 7.0.7 Built on CentOS 7, parallel computation pyscript mpi exit error? | EternalSeekerX | SU2 | 3 | October 9, 2020 19:28 |
| Problem of simulating of small droplet with radius of 2mm | liguifan | OpenFOAM Running, Solving & CFD | 5 | June 3, 2014 03:53 |
| Gradient evaluation in Finite Volume Methods | yidongxia | Main CFD Forum | 7 | August 6, 2012 11:23 |
| Unstructured grid finite volume methods | Marcus | Main CFD Forum | 3 | December 5, 2000 01:25 |