 |
|
|
[Sponsors] | |||||
Calculating energy dissipation rate from power spectrum |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 | |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
Quote:
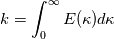 I am confused about how the distribution of eddy sizes (independent of the energy they contain) is included in this equation. Does the eqn only include the total energy of eddies of a particular size without knowing how many of these eddies there are relative to the the total number of eddies? Or is the size distribution inherently included in the equation? |
||
|
|

|
||
|
|
|
#22 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
an element 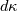 has the dimension l^-1. That means that while integrating along the spatial frequencies you are evaluating the contribution of energy due the whole range of eddies. has the dimension l^-1. That means that while integrating along the spatial frequencies you are evaluating the contribution of energy due the whole range of eddies.
|
|
|
|

|
|
|
|
|
#23 |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
||
|
|

|
|
|
|
|
#24 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
||
|
|

|
|
|
|
|
#25 |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
As a very hypothetical example (no doubt removed from reality) something like there twice as many eddies of size 1 as there are of size 2 which number five times as many as eddies of size 3 and so on. Something like that. Or maybe a Gaussian distribution where the number of large eddies and Kolmogorov eddies are small, but there is an eddy size somewhere in the middle where the number of those eddies is the highest.
|
|
|
|

|
|
|
|
|
#26 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
I don't know if that has some sense, you have a continuous creation, stretching, stirring and dissipation of eddies. In some problems you have also a reverse mechanism with larger structures produced by smaller one. Note that an identification of a vortical structure is still a problem, then you should attribute also the statistical meaning of coherence to discriminate the relevant number of structures. At present, I don't remember if literature has some work with the analysis of the statistical distribution. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Constant Residual of Turbulence Kinetic Energy and Dissipation Rate | wrightguy | FLUENT | 4 | June 20, 2021 11:19 |
| Energy spectrum in frequency | bhigahAshish | Main CFD Forum | 4 | July 7, 2019 11:54 |
| ATTENTION! Reliability problems in CFX 5.7 | Joseph | CFX | 14 | April 20, 2010 16:45 |
| calculation of (turbulent) dissipation energy ? | max | Main CFD Forum | 3 | August 18, 1999 10:42 |
| Why FVM for high-Re flows? | Zhong Lei | Main CFD Forum | 23 | May 14, 1999 14:22 |