 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Suppose I have the linear system:
rho_t+Urho_x+rho_0v_x=0 v_t+Uv_x=Dv_xx+aT_x T_t+UT_x=kT_xx+bv_x This is a mixed system of equations, one hyperbolic and two parabolic. I thought about upwinding the first-order derivatives and doing central difference for the second-order derivatives. The domain is for 0<=x<=1, and t>0. The method I used failed completely, I was using explicit Euler, with a low CFL number to get convergence, but the results were haywire. Any suggestions on how to get started? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
If I understand your notation, U should be U0=constant. In the momentum equation you have substituted the pressure gradient by means of the EOS? Then grad p= R grad (rho_0+rho)(T0+T) has the minus sign in the RHS. |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
For the moment, I don't want to consider such things, as the actual system I'm dealing with is somewhat complicated.
U is constant, I wanted to make my system simple. I did upwinding for all first-order derivatives and central differencing for the second-order derivatives. I then solved this using explicit Euler using small timesteps and slow speeds and I just got complete junk. I'm at a loss as to what to do. |
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
you havent answered to my question about the pressure gradient |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I have, simply ignore the pressure gradient for now. The system I put in the OP was a representative set of equations that I wish to solve. This is a question on pure numerics. The issue is that I have one hyperbolic equation, and two parabolic equations.
|
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
You added arbitrarily two source term, now depending on you prescribed BCs are you sure a solution exists?
|
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
The source terms aren't arbitrary but are dependent upon the model that these linear equations are meant to represent. The temperature gradient in the second one represents thermal stress, which couples temperature to the other variables. The velocity gradient comes in from the thermal stress as well in deriving the temperature equation from thermodynamics.
As for BCs, I have one end fixed and the other is stress-free (so one end is allowed to move), I have Dirichlet conditions for the temperature at each end. For the density, I have the density gradient at x=1, to be zero and I have no boundary condition for the other end. I think that should be reasonably physical and representative of the physical system I hope to solve once I get the linear system working. |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,753
Rep Power: 66    |
If you choose the correct a and b, this would be identical to a reduced form of navier-stokes with a background flow U. You have "removed the pressure gradient" but replaced it with a momentum source which would mimic exactly the same pressure gradient that you would have had. Keep in mind the work-energy theorem.
You have a coupled system of PDE's, it's not a linear system until you discretize it. But discretizing with explicit euler should lead to a marching forward in time procedure, not a linear system. Are you sure you are solving a linear system? |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Ok, let us have a step back. You start from the NSE equations for compressible flows d rho/dt+ u*drho/dx+rho*du/dx=0 du/dt + u*du/dx+(1/rho)*dp/dx= ni*d^2u/dx2 d(rho*E)/dt + d/dx (rho*u*E + p/rho)=k*d^2T/dx^2 +4/3*mu*d(u*du/dx)/dx E=u^2/2+Cp*T and then introduce a linearization? How do you get your final linear system? |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I am absolutely positive that the system is linear.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
The system wasn't a reduction of the Navier-Stokes equations, but a set of linear equations that mimic the Navier-Stokes equations.
|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
This is not my doubt, linearization is a mathematical procedure you can introduce. Of course, one could argue if it is physically correct for the problem you want to solve, but I assume that all fluctuations in your problem are small so that we can focus on the numerical issues of your question. 1) My question is how do you get your linear system of equations when you introduce the linearization in the NSE I wrote above. 2) For small viscosity and conducibility values you have a perturbed set of hyperbolic linear equations. According to the direction of the characteristic lines, you have to be careful in the BCs. 3) Have you first tested the standard case of the linear hyperbolic Euler equations where you have an exact solution? 4) have you considered the stability constraint for the diffusive terms Then, you could give more details about the problems you see in your numerical solution, with some plots |
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
Why the title of your post is "compressible flows"? Again, how do you want to judge the quality of your solution on such a system of equations? Have you found an analytical solution before? |
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
1) My question is how do you get your linear system of equations when you introduce the linearization in the NSE I wrote above.
I explained this before. There was no linearisation. The equations were put forward as a stand alone system designed to mimic the set of nonlinear equations I am hoping to solve. I wanted to start easy, so I wrote down a set of linear equations that I thought would be easy to solve. 2) For small viscosity and conducibility values you have a perturbed set of hyperbolic linear equations. According to the direction of the characteristic lines, you have to be careful in the BCs. Only one is hyperbolic, the others are parabolic, having only a second-order spatial derivative. That's the big issue that I am looking at currently. 3) Have you first tested the standard case of the linear hyperbolic Euler equations where you have an exact solution? Not relevant as I have explained before. 4) have you considered the stability constraint for the diffusive terms I'm not too sure what you mean by this. Could you explain what you mean a little more? |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
Why the title of your post is "compressible flows"?
The original set of equations was essentially looking at a 1D compressible elastic rod that shrinks under heating. Again, how do you want to judge the quality of your solution on such a system of equations? Have you found an analytical solution before? As it's on a finite domain, it has to be solved using Fourier series, and then you're into looking at how many terms you take. |
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
In your equations you have convection, diffusion and production terms. Each one has its stability constraint. You cannot use only the cfl condition. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
There is a methology for non-conservative products called path-conservative schemes, which might useful for you. The method can be applied to systems of the form
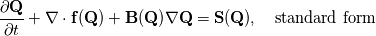 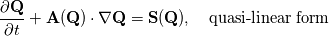 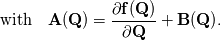 Here 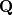 is the conservative state vector, is the conservative state vector, 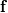 is the conservative flux vector (which may also contain parabolic terms is the conservative flux vector (which may also contain parabolic terms 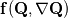 ) and ) and  is a source term. The third term in the first line is the non-conservative product. In case of is a source term. The third term in the first line is the non-conservative product. In case of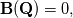 you recover the well known conservation law. You may read some papers of LeFloch, Parès or Castro. [1],[2] Regards |
|
|
|

|
|
|
|
|
#18 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,753
Rep Power: 66    |
I try to avoid semantic arguments but it is creating confusion. A "linear system" generally means a system of linear algebraic equations which needs to be solved via gaussian elimination, etc.
Your equations are indeed linear in U and T because it is a linearized system of PDE's. But it isn't a "linear system" that you learn in high school algebra. You are referring to the linear vector property of functionals. We are taking about linear systems (of equations). Convective terms have CFL stability constraint. Diffusive terms have Fourier number constraints. So after discretization, you end up with what? A system of equations or just a marching procedure? Can you show it? |
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
Matthew
Join Date: Mar 2022
Location: United Kingdom
Posts: 184
Rep Power: 4  |
I don't know what you think a linear system should look like. My background is mathematics, it's a linear system of equations to me.
I discretised the system using finite differences. I used a forward difference for all first-order derivatives and central difference for all second-order derivatives. |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Your system can be written like
u^n+1 = T.u^n Where u is the state vector. If you do the stability analysis on the eigenvalues of T you will be able to understand that the CFL is not the only parameter to check. |
|
|
|

|
|
 |
| Tags |
| 1dfluid, cfd |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Compressible nozzle flow - no problem for fluent but impossible with openFOAM? | flar.t | OpenFOAM Running, Solving & CFD | 10 | March 30, 2022 02:21 |
| Compressible flow, no data at the outlet | mireis | FLUENT | 6 | September 3, 2015 03:10 |
| Natural Convection using Compressible Flow (chtMultiRegionFOAM) | msarkar | OpenFOAM | 2 | September 7, 2010 01:13 |
| help with compressible flow BC's (need subsonic flow) | meangreen | Main CFD Forum | 5 | July 24, 2010 14:16 |
| Solving unsteady compressible low speed flow | atit | Main CFD Forum | 8 | July 31, 2000 14:19 |