 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Manos Dimitriadis
Join Date: May 2023
Posts: 20
Rep Power: 3  |
Hi all,
I have a question that I have not found in any literature answered clearly. Is Spalding law and Musker accurate for describing mean velocity profiles in rough surfaces in turbulent boundary layers? Thanks |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
No, at least not in their known form.
I don't know for Spalding but, for Musker it is possible to introduce a transformation of its two parameters (k and a) that will, for example, make it adapt to arbitrary Pr/Pr_t ratios and thus make it a thermal wall function. As a consequence, I think that, at least for Musker, it is probably possible to introduce a similar transformation for the effects of roughness. I somehow worked extensively on this thermal part (checkout my related blog posts here on cfd-online) but haven't had time yet to work on the roughness part. I'm confident about this because I was also able to brute force adapt the Musker profile to several turbulence models by acting on the same profile parameters. In the end, it is just the logarithmic intercept (according to the common view on roughness) that needs adaptation, which is controlled by the parameter a. |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Manos Dimitriadis
Join Date: May 2023
Posts: 20
Rep Power: 3  |
Quote:
Is there any limit for how smooth wall boundary layer could be in which both expressions at their original forms would provide a good fit to data? Because e.g. for the Spalding expression most research works implement the boundary layer constant of k=0.41 and B=5.0 and do not deviate far from these. |
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
|
Quote:
However, in practice, what I wanted to say is that using the two free parameters in the Musker profile you can fit it to a certain family of profiles which I expect to inlcude the roughness effects. I don't know of any specific limits if not those for the underlying roughness. That is, the profiles will be probably good in the smoothness regime, which is up to k+ around 5. My experience with Musker and the related references gives k=0.384 and a=10.306 as best fitting constants for the turbulent channel flow. I have a corresponding standard logarithmic constant calculated somewhere, but I will have to look for that |
||
|
|

|
||
|
|
|
#5 | |
|
New Member
Manos Dimitriadis
Join Date: May 2023
Posts: 20
Rep Power: 3  |
Quote:
I have seen k=0.384 and a=-10.3061 for constants in the publication "Criteria for assessing experiments in zero pressure gradient boundary layers" but still I think they refer to smooth wall BL |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
|
Quote:
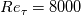 and I confim them to be the best ones for this case as well. Obviously, this is far from an objective assessment, as it deends on the specific criterion adopted etc., but my very point is that they are, indeed, relevant for turbulent channels as well. and I confim them to be the best ones for this case as well. Obviously, this is far from an objective assessment, as it deends on the specific criterion adopted etc., but my very point is that they are, indeed, relevant for turbulent channels as well.Again, I have no direct experience on the adaptation for roughness but, honestly, every single work I've seen on that just models the logarithmic constant. And, what I want to highlight here is that, in my experience, the constants in the Musker profile can easily cover that same variations. So, the Musker profile has the potential in my opinion, but I don't know of any specific study on that. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
|
If you look at the Spalding derivation, however, it is clear that its formula also has the same potential, as probably all the formulas out there, because they all are devised to match a specific logarithmic behavior for large y+. The point thus is simply converting the roughness effect on the classical logarithmic profile into the new formulas.
Note however that having a very small y+ (something that would require an all y+ formulation as those of Spalding or Musker) is kind of in contradiction to the roughness modeling trough wall functions. I can only see a sense in the fact that they are better behaved functions that just a forced logarithmic one, but this is more numerical than anything else and you should avoid, in my opinion, working with small y+ values in case of high roughness. I have a number of papers sitting around on these topics. As time has passed, it's difficult to suggest one in particular now. From a rapid check, maybe, you want to give a look at this one in particular: https://www.sciencedirect.com/scienc...42727X19306393 |
|
|
|

|
|
 |
| Tags |
| musker, roughness sand grain, spalding |
|
|