 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
I have built a pressure projection FVM solver for incompressible flow, and it works as intended if I use a small gravitational force, like 0.01 * 9.81. But when I use a larger value, like the actual acceleration of gravity of 9.81, the solver becomes very unstable and blows up.
I built the code without any third part libraries, so my question is conceptual... I would like to know what stability condition I am missing... My code is fully implicit for both the advection and diffusion term. I was using Crank Nicolson semi-implicit but realized that fully implicit is more stable. I tried a pressure correction approach and it still failed at 9.81 source value. I might try to damp the pressure corrector, as I think that the large source term is causing the pressure to over correct and leading to large errors. Any suggestions would be helpful. My ultimate goal is to create an unconditionally stable incompressible solver for natural convection. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
Do you have variable density and/or temperature?
Are you using a boussinesq like term or full gravity? Usually, for full gravity, one splits it in a constant density term absorbed by the pressure and a variable density one, which should be more benign. Fully coupled scheme then make it implicit as well |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
There are many possible issues in the projection method for bouyancy-driven flows. I assume that you validated carefully your code in standard solution without bouyancy. You should detail how you solve the system, are you solving the internal energy equation with the Bousinnesq coupling? How do you discretize the source term in time? Is the non linear term linearized in the implicit scheme? |
||
|
|

|
||
|
|
|
#4 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
I am using a boussinesq like term: 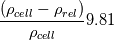 The density is calculated at each time step based on temperature, using the equation of state for air. I solve an energy equation for the temperature as part of the procedure to get the density. Can you describe what you mean by "make it implicit as well"? |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
||
|
|

|
|
|
|
|
#6 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
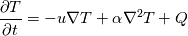 Then I use the equation of state for air to get a density field. Then the fully implicit momentum equation: 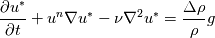 I make the convection term linear by using the previous time step velocity. In matrix form it looks like this: ![\left[ \frac{1}{\Delta t} \right] \left[ u^{*} \right]
+
\left[ u^{n}\nabla \right] \left[ u^{*} \right]
+
\left[ -\nu \nabla^{2} \right] \left[ u^{*} \right]
=
\left[ \frac{\Delta\rho}{\rho} g + \frac{ u^{n}}{\Delta t} \right] \left[ \frac{1}{\Delta t} \right] \left[ u^{*} \right]
+
\left[ u^{n}\nabla \right] \left[ u^{*} \right]
+
\left[ -\nu \nabla^{2} \right] \left[ u^{*} \right]
=
\left[ \frac{\Delta\rho}{\rho} g + \frac{ u^{n}}{\Delta t} \right]](/Forums/vbLatex/img/392129850c6e27a1ed1773987562de0b-1.gif) I then solve the pressure poisson equation with zero divergence for the 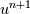 term, and solve for term, and solve for 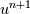 using the gradient pressure. using the gradient pressure.
|
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Why do you use the state equation?
When you solve the temperature field, the buoyancy term in the momentum is expressed directly by the temperature. Be also careful, the time step you must use is dictated by the explicit scheme in the temperature equation, your implicit scheme cannot use an arbitrary high time step. The stability in the temperature equation depends on the Peclet and cfl but for the momentum equation the source term has influence on the stability. Before introducing the bouyancy term what kind of test case have you resolved to assess the omothermal case? |
|
|
|

|
|
|
|
|
#8 |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
||
|
|

|
|
|
|
|
#9 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
From what I understand, the bousenessq term is derived from the equation of state anyway. I just use density variation instead of temperature variation. I can substitute the actual bousenessq term in my equation and the same results occur. |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
|
Quote:
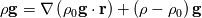 where the first term, with a suitably chosen value for the reference density 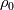 , can be included in the pressure gradient. The second term then will be less troublesome. , can be included in the pressure gradient. The second term then will be less troublesome.Second, a coupled solver will typically handle all the equations together. For example, a preconditioned density based code has 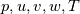 as vector of independent variables and the matrix coefficients are 5x5 blocks, so a momentum source term depending on density has an explicit dependence from the independent variables and I can treat it implicitly with no particular reasoning. as vector of independent variables and the matrix coefficients are 5x5 blocks, so a momentum source term depending on density has an explicit dependence from the independent variables and I can treat it implicitly with no particular reasoning.In your case, density is function of T, whose equation is not solved with momentum but segregated. The stability analysis here is more complex, and I have no direct experience, but solving for the temperature first should already give you a better stability. |
||
|
|

|
||
|
|
|
#11 | |
|
Senior Member
|
Quote:
With Boussinesq you can use a constant density code. Without it, you need a variable density one. |
||
|
|

|
||
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Solve first for the temperature, then you have the temperature solutions both at tn and tn+1 to insert into the momentum by means of Bousinnesq.
However, check that the stabilty constraint is satisfied for the temperature equation. |
|
|
|

|
|
|
|
|
#13 |
|
Member
EM
Join Date: Sep 2019
Posts: 59
Rep Power: 7  |
*important*: since u have incompressible flow, your buoyancy term *must* obey the pressure compatibility condition otherwise your discrete system has no solution. once fulfilled, the B-V frequency below is the next consideration. Brunt-Vaisala instability. Even if u do not explicitly impose stable stratification, thermal flows will develop regions (at least transiently) where these occur. There is no steady state solution and codes will never converge to a steady-state. If timestepping is used, u must time-resolve those gravity waves or up it goes. these numerical effects have been known for quite a while. Last edited by gnwt4a; May 23, 2023 at 04:43. Reason: Added compatibility precondition |
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#15 | |
|
New Member
Join Date: Nov 2013
Posts: 5
Rep Power: 13  |
Quote:
Regarding your last statement: is that really so? shouldn't be also possible to use an EoS for the buoyancy term rho*g in an incompressible (constant density) setting? I guess the results should be pretty similar (if not the same) if a incompressible solver is used together with an EoS, or a linearized form of it... at least for very small temperature differenecs |
||
|
|

|
||
|
|
|
#16 | |
|
Senior Member
|
Quote:
Boussinesq is not an arbitrary EOS, it is, specifically, a linearization of a density depending only from temperature around a given temperature. It is arbitrary in the thermal expasion coefficient, indeed, not the rest. That's where your freedom is in using Boussinesq. So, if you are using a general density form but only in the gravity term, it certainly is a mistake. Is it the cause of your instability? I don't know. But it might be. |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
And how do you think you can compute rho=p/RT ? How do you evaluate "p" in the incompressible flow model? |
||
|
|

|
||
|
|
|
#18 | |
|
New Member
Join Date: Nov 2013
Posts: 5
Rep Power: 13  |
Quote:
I'm really not sure if it makes sense, but wouldn't it be possible to just use for the pressure appearing in the EoS a constant pressure (the thermodynamic pressure) , as it is done in the low-Mach formulation of the governing equations? |
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
You donít have any thermodynamics law in the incompresdible flow model.
|
|
|
|

|
|
|
|
|
#20 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
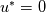 and and 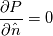 . I set an arbitrary pressure at one point, P = 0, and I always get a unique solution for the poisson system of equations. I use P = 0 because I'm only interested in the pressure gradient, not absolute pressure. This is typical for walls, correct? I tried to find literature on "pressure compatibility condition" and I cannot find anything useful. Do you have a source for this? . I set an arbitrary pressure at one point, P = 0, and I always get a unique solution for the poisson system of equations. I use P = 0 because I'm only interested in the pressure gradient, not absolute pressure. This is typical for walls, correct? I tried to find literature on "pressure compatibility condition" and I cannot find anything useful. Do you have a source for this?Brunt-Vaisala instability might be what I am experiencing... I looked at the Wikepedia article for it and I understand the general concept. Is there a way to eliminate this stability condition? Last night, I ran the simulation for 12 hours (around 100,000 iterations & 1,072 simulated flow seconds). It's perfectly stable with a body force term of 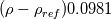 . By keeping the gravity term low, I notice the lack of "swirling" or curling in the simulation. When I bump up the gravity term to the correct 9.81 value, I get swirling effects and eventual very high velocities that blow up. The simulation usually fails within 30 seconds. . By keeping the gravity term low, I notice the lack of "swirling" or curling in the simulation. When I bump up the gravity term to the correct 9.81 value, I get swirling effects and eventual very high velocities that blow up. The simulation usually fails within 30 seconds.
|
||
|
|

|
||
 |
| Tags |
| finite volume method, implicit, incompressible flow, pressure projection |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [foam-extend.org] Problems installing foam-extend-4.0 on openSUSE 42.2 and Ubuntu 16.04 | ordinary | OpenFOAM Installation | 19 | September 3, 2019 19:13 |
| [Other] How to use finite area method in official OpenFOAM 2.2.0? | Detian Liu | OpenFOAM Meshing & Mesh Conversion | 4 | November 3, 2015 04:04 |
| [swak4Foam] Swak4FOAM 0.2.3 / OF2.2.x installation error | FerdiFuchs | OpenFOAM Community Contributions | 27 | April 16, 2014 16:14 |
| [swak4Foam] Error bulding swak4Foam | sfigato | OpenFOAM Community Contributions | 18 | August 22, 2013 13:41 |
| [swak4Foam] build problem swak4Foam OF 2.2.0 | mcathela | OpenFOAM Community Contributions | 14 | April 23, 2013 14:59 |