 |
|
|
[Sponsors] | |||||
|
|
|
#21 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
In your experience, do buoyancy driven flow problems have this same issue? The system I am simulating is fully enclosed, with a heat source in the center. I would like to know if the issue is stability, my setup, or something else. Given that small gravity forces work fine, I can't see how my discretization is incorrect. I really think that pressure is overcorrecting the large acceleration from gravity, and by forcing zero divergence on large accelerations, the pressure is creating nonphysical velocities. I would like to create multiple steps within the pressure projection method to compensate for the overcorrection. If I can break up the contribution of pressure into two steps then maybe the projection method can handle the large acceleration term. This is my first time working with CFD, so I would like some pointers so I don't waste too much time guessing. I was wondering why other buoyancy flow codes don't discuss this issue. I can't find any literature on source term stability for incompressible flows. |
||
|
|

|
||
|
|
|
#22 |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
I don't know who "jpanchog" is, but it's not me. I will use the Boussinesq term instead of the density term for gravity. But that's not really the concern right now, I really just want to understand why a large body force is throwing off the simulation... how is this not an issue for other CFD codes? How are they dealing with it? And why can't I find anything in the literature about it?
|
|
|
|

|
|
|
|
|
#23 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
First of all, could you address the values for the characteristic non-dimensional numbers Peclet and Rayleigh? The first test you have to try is to prescribe a stable initial condition, that is a temperature distribution that, for any value of Rayleigh, is not changed by your code. That means the code recognizes the stable solution a provides the steady state at the first time step. Are you working using a second order scheme? On staggered or non-staggered grid? I worked without any problem with buoyancy driven flows. |
||
|
|

|
||
|
|
|
#24 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
I based my code on this paper: https://repository.tudelft.nl/island...m/OBJ/download It's a staggered approach, but with delaunay triangles as the pressure cells, and quadrilaterals as the velocity cells. My model is 2D but the principle is the same. The quadrilaterals are centered on the edges of the triangular pressure cells. Careful attention is taken to ensure that the velocity has zero divergence. I check divergence with each iteration, and it is usually around  . . The pressure poisson matrix in this method is also very stiff, which I would assume would mean more accurate and stable. The pressure of one cell takes into consideration three surrounding cell pressures, and two more additional pressure cells each, for a total of 9 pressure cells, rather than the typical 3 in the SOE. I have triple checked that the gradients are calculated correctly, however, even if they were wrong, it would just produce a wrong solution. That doesn't necessarily mean the solution would blow up. I find it strange that my code works for small gravity values, but not for large ones. Are you asking me to provide the Rayleigh and Peclet numbers when the simulation fails? |
||
|
|

|
||
|
|
|
#25 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
The pressure matrix is singular, this is correct for the Neumann BCs the pressure problem requires. As already addressed, the numerical stability region for a convection-diffusion-production term has different features from the simple convection-diffusion equation. High Ra values can require very low time step. The flow problem you should first test is the simple cavity with adiabatic vertical walls and heated bottom wall. Use the low Ra values you can find in the well known literature for such a test. You should easily check if you have some problem in your code starting from the rest and initial constant temperature field. |
||
|
|

|
||
|
|
|
#26 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,763
Rep Power: 66    |
It is quite apparent that your code is not stable without needing to do a PhD on the topic. You've told us so. Let's move on.... and actually start looking into how stable your code actually is rather than stubbornly being fixated on it being stable when it likely is stable and unstable when it clearly is.
Shallow water wave equation and the dam break problem are quite vast sources of literature on stability that you seemingly cannot find anything on. Just like pressure problem, you get fast and slow gravity waves. The speed of the slow waves (which, just like pressure, can cause a lot of problems) goes like the square root of the hydraulic energy grade line and this is the number that needs to be added to your Courant number. Clearly, schemes cannot be stable to arbitrarily high g unless the scheme can tolerant infinite Courant numbers. |
|
|
|

|
|
|
|
|
#27 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
If I'm wrong, then please point me to a formulation of the Co for stability based on the buoyancy source term. Also, I'm not sure why dozens of papers on buoyancy driven flows don't include stability analysis outside of the typical Courant formulation. I don't see why I should need to reference a less common problem of a "dam break" to find an answer for a natural convection problem. I understand, on a conceptual level two things: 1. Infinitely larger body forces seem unlikely to be unconditionally stable. 2. The stability of the buoyancy problem probably has to do with a few factors: the gradient of temperature from one cell to the next, the cell shape and size, and 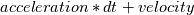 (which would describe the transport of info from one cell to the next) (which would describe the transport of info from one cell to the next)Ideally I would not have a stability constraint for the buoyancy term. If there's a specific paper or website you have in mind, please post the link. |
||
|
|

|
||
|
|
|
#28 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,763
Rep Power: 66    |
The gravitational force creates flow.... there's your advection.
Implicit schemes are also unstable, especially so when you have anything more than small linear perturbations. You're also using a segregated approach, so you aren't even fully implicit. Only specific implicit schemes are stable, not all of them. The dam break problem is the classical problem giving gravity waves and that's why I suggest since you ask specifically about why large values of gravity can cause a problem to become unstable. I am sorry you are not interested in the answer that you seek. I'm not interested in any argumentum ad populum debate. If you really understand that infinitely large forces are unlikely permastable, doesn't that seem to contradict your own statement? If you imagine that I put in an arbitrarily large forcing term (and label it banana instead of g), you expect every implicit scheme to always be stable? I'm also giving you the courtesy of assuming that you are not completely wrong about everything and that you code is even coded properly So are we here to debate why you code is unstable when it clearly isn't working or can we actually see the characteristics of your problem? Rayleigh numbers, Peclet numbers, Courant numbers? Please? Last edited by LuckyTran; May 23, 2023 at 22:46. |
|
|
|

|
|
|
|
|
#29 | ||||||
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
Quote:
Quote:
Quote:
Does the stability of the temperature equation become unstable with large heat generation (source term)? No, although it can become inaccurate. That's because increasing heat generation does not relate to the rate of information travelled, unlike the diffusion and advection term in the temperature equation. Stability for heat transfer equation is:  for diffusion for diffusion for advection for advectionAnyway, after all this thinking, I believe I managed to formulate my own stability criteria for the boussinesq equation. I plan on running my simulation over night at full gravity (9.81). My next step, which is my actual goal, is to find a way to make it implicit, possibly by coupling the heat and momentum equations together. I'll take a look at dam break papers and see if I can gather anything from them. Quote:
Quote:
Remember, I am new to CFD. A lot of these problems I encounter have to dealt with one by one, and I often have problems searching for answers online because I don't know the nomenclature. Turns out you have to know the names of things in order to find them online. |
|||||||
|
|

|
|||||||
|
|
|
#30 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,763
Rep Power: 66    |
Yes of course your code has absolutely no potential of being incorrectly coded and it is unconditionally stable for all possible problems in the universe. Periodt. What a dream.
|
|
|
|

|
|
|
|
|
#31 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
Quote:
This is absolutely false and also contradicts your question as to how it is stable for other softwares since flows with gravity has been solved all the time. Obviously it can be run in other codes at much higher dt than you are running. Having said this, what Lucky said is true ie at certain values of body forces almost all the codes would break down. Finite analytical methods probably would not break down or take much larger values because they are analytical method for most part. To answer your question: 1. Body force based calculations are notorious for being unstable. 2. Most people do not use projection methods so they don#t face problems you face. For example none of big softwares is projection method based. They are correction based methods. 3. If you are hundred percent sure that code has no bugs and everything is right then try splitting method. If i were you i would split the momentum solve into two steps. First with only body force and then momentum without body force. Since with body force only it shall be easy to solve and you might write down analtical values after the step is taken since now du/dt = gr only. |
||
|
|

|
||
|
|
|
#32 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
A.f_n+1=B.f_n + k g_n C.g_n+1=D.g_n Insert the matrices for your case in these two linear equations and perform the von Neumann stability analysis. |
|
|
|

|
|
|
|
|
#33 |
|
Senior Member
|
I think the matter here is far from trivial. There are too much elements in your case that are non standard (starting from the code itself).
Please remove the heat source and do some more traditional tests on the thermally driven cavity. I would actually start from stable stratification and then the opposite. Only if those works then you can get back to the original problem. Ad I said, I work with coupled solvers, wherenthe gravity term can be treated implicitly as any other term. When I wasn't using the implicit treatment the gravity was, indeed, very unstable. |
|
|
|

|
|
|
|
|
#34 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
I ended up splitting each momentum term into its own step, as is done in Fast Fluid Dynamics (FFD). I use a high order semi-lagrangian scheme for the advection step. The diffusion step is still implicit. It works well, but I'm still trying to increase its speed. There are obvious ways to increase the semi-lagrangian compute speed with multithreading, but the pressure projection step is still the real bottleneck. It's an order of magnitude slower to compute than the other steps. Increasing the time step is possible, but the accuracy suffers a lot. No matter how high order the advection semi-lagrangian scheme is, the accuracy decreases with larger time step due to the semi-langrangian being a characteristic method. Does anyone know which iterative solver is the quickest for pressure poisson equation on unstructured grids? If I use a structured grid for pressure, I know the matrix breaks down into chunks based on row size, which can be easily parallelized with multithreading -- using TDMA or something similar. But the pre and post processing of the pressure might become the new bottleneck. |
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
|
Quote:
What kind of verification have you done for your code before this? At this point, considering that you mentioned being a CFD novice, this is the most important step. Nobody starts verification from a buoyancy case. |
||
|
|

|
||
|
|
|
#36 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,291
Rep Power: 35   |
pressure solver is bottleneck of unstructured solvers for long time. in your case you might want to consider some lib that provides good amg solver.
Quote:
|
||
|
|

|
||
|
|
|
#37 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
I'll be creating an energy conservative semi-lagrangian scheme for the convection term in the temperature/energy equation, since this is another stability, and speed, bottle neck. Thermal convection with semi-lagrangian is unconditionally stable, but it will need to be conservative unlike the velocity. Thermal energy conservation is vastly more important than conserving velocity, given that my ultimate goal is heat transfer analysis. After all that, I'll be adding an AMG solver for pressure. |
||
|
|

|
||
|
|
|
#38 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
First of all, internal energy is not physically conserved. Then, the conservative property of a numerical scheme is relevant in the discretization of quadratic non-linear flux of momentum since it ensures the correct propagation of convective Waves. |
||
|
|

|
||
|
|
|
#39 | |
|
New Member
Join Date: May 2023
Posts: 15
Rep Power: 3  |
Quote:
My point is only that I cannot use the semi-lagrangian method in the temperature equation unless I can find a way to make it thermally conserving. This is especially important for long running simulations. |
||
|
|

|
||
 |
| Tags |
| finite volume method, implicit, incompressible flow, pressure projection |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [foam-extend.org] Problems installing foam-extend-4.0 on openSUSE 42.2 and Ubuntu 16.04 | ordinary | OpenFOAM Installation | 19 | September 3, 2019 19:13 |
| [Other] How to use finite area method in official OpenFOAM 2.2.0? | Detian Liu | OpenFOAM Meshing & Mesh Conversion | 4 | November 3, 2015 04:04 |
| [swak4Foam] Swak4FOAM 0.2.3 / OF2.2.x installation error | FerdiFuchs | OpenFOAM Community Contributions | 27 | April 16, 2014 16:14 |
| [swak4Foam] Error bulding swak4Foam | sfigato | OpenFOAM Community Contributions | 18 | August 22, 2013 13:41 |
| [swak4Foam] build problem swak4Foam OF 2.2.0 | mcathela | OpenFOAM Community Contributions | 14 | April 23, 2013 14:59 |