 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Hi everyone,
I am looking for some help in solving a problem I face in solving the Euler equations (more or less). I have looked and looked but up to now I have not found a functional solution. The scenario I am trying to simulate is actually a little bit more complex than the usual inviscid Euler equations: I am solving a time dependent multifluid 2D problem where I consider a plasma composed by ions and electrons. The two fluids are coupled through the electric field solved with the Poisson equation. Everything is immersed in a uniform magnetic field. To have an idea, each specie (ions and electrons) obeys the Euler equations with non zero sources on the rhs, in particular I have a mass injection, electric and magnetic field effects. I solve for the conservative variables. To complicate things even more, the scenario I am simulating results in supersonic and subsonic regions, extremely large velocities in some points and very low densities, reaching near vacuum conditions. I have successfully run this simulation with a Rusanov scheme with 2nd order MUSCL reconstruction and an unsplit scheme, with a third order SSP Runge Kutta integration. The Rusanov fluxes are positive preserving so that I never reach negative densities and everything works (more or less). However, since I am trying to evaluate the occurrence of turbulent effects, the Rusanov flux is too dissipative and the results are "contaminated" by numerical diffusion. I then coded Riemann solvers utilizing more waves, in particular both the Roe and the HLLEM and I am currently using the last one, with 2nd order MUSCL reconstruction on primitive variables and MINMOD or VanLeer limiters. (the code is a home made solver written in fortran with structure meshes). With the HLLEM however, given that the numerical diffusion is strongly reduced with respect to Rusanov, the simulation hardly manages to complete, mostly because I obtain a negative temperature under square root. I know that the issue of positivity preserving is problematic, especially dealing with flows where the total energy is close to the kinetic energy, so that computing the temperature may lead to negative values. What I am trying to do is to switch to the more diffusive Rusanov, or even 1st order Rusanov, scheme when I detect negative values, thus recomputing the time step. I even tried using such scheme in regions of the domain where I know I will have problems, near the boundaries, but I get weird effects at the interface between the two schemes and the problem arises again. The biggest issue seems to be the computation of the temperature itself, density and energies, even pressure are smooth, but when I compute the temperature it is highly discontinuous in low density regions. My feeling is that i suffer from catastrophic cancellation in subtracting the kinetic energy from the total energy and once I divide by the density all the errors come up. I am not sure on how to proceed from here since I cannot think of a way to prevent this. I even thought about having some sort of tracking interface where in one side I have density and in the other vacuum where I don't solve anything, but is this even possible? I know that I am stretching the fluid approximation itself, but this is exactly the point. Since I have limited experience on the subject I might have lost something. Is there any solution or technique, switching or trick that I can apply to avoid the temperature to become negative or in general blowing up ? thanks, Davide |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Can you write down some equations of your model? Do you have a one energy/density/velocity model or more transport equations for each species?
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Sure, here you can see the general form of the system of equations which is solved for each specie.
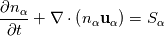 ![\frac{\partial \left(n_\alpha \textbf{u}_\alpha\right)}{\partial t} + \nabla \cdot \left(\left(n_\alpha \textbf{u}_\alpha\right)\textbf{u}_\alpha\right) = \frac{qn_\alpha}{m_\alpha}\left[\textbf{u}_\alpha\times \textbf{B} + \nabla \phi\right] - \frac{1}{m_\alpha}\nabla P_\alpha \frac{\partial \left(n_\alpha \textbf{u}_\alpha\right)}{\partial t} + \nabla \cdot \left(\left(n_\alpha \textbf{u}_\alpha\right)\textbf{u}_\alpha\right) = \frac{qn_\alpha}{m_\alpha}\left[\textbf{u}_\alpha\times \textbf{B} + \nabla \phi\right] - \frac{1}{m_\alpha}\nabla P_\alpha](/Forums/vbLatex/img/57504da0d5591903cb669b961eb68202-1.gif)  The system can be easily recast in the "standard" form of the Euler equations. In this case n is the number density, E is the total energy (not specific), q is the charge (  e, the elementary charge), e, the elementary charge), 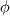 is the electric potential and B = B_z z the uniform magnetic field perpendicular to the domain (x,y). is the electric potential and B = B_z z the uniform magnetic field perpendicular to the domain (x,y). Moreover 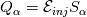 is the injection energy times the injection source term. is the injection energy times the injection source term.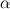 denotes either the ions and electrons which are integrated in time separately, advanced of one step in each algorithm loop. The two systems are coupled through the Poisson equation : denotes either the ions and electrons which are integrated in time separately, advanced of one step in each algorithm loop. The two systems are coupled through the Poisson equation : Just as a reference, for Xenon (as an example) 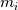 = 2.18e-25 kg while = 2.18e-25 kg while 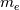 = 9.1e-31 kg, which leads to a huge difference in timescales for ions and electrons, as well as very different sound speeds (given that electrons have temperatures 1-2 orders of magnitude larger than ions). Moreover in order to solve the non neutrality of the problem, the debye length and plasma frequency must be resolved, which usually forces the timestep to be extremely small. I am currently using between 0.5 and 10 ps. = 9.1e-31 kg, which leads to a huge difference in timescales for ions and electrons, as well as very different sound speeds (given that electrons have temperatures 1-2 orders of magnitude larger than ions). Moreover in order to solve the non neutrality of the problem, the debye length and plasma frequency must be resolved, which usually forces the timestep to be extremely small. I am currently using between 0.5 and 10 ps.
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Maksim
Join Date: Jul 2020
Posts: 10
Rep Power: 6  |
Have You tested your code with Noh test? It's a test, where you can check, how small internal energy can be comparing to kinetic energy in your scheme.
Also what variables do You reconstruct? Density, velocity and pressure? |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Hi, thanks for the reply.
No I didn't try the Noh test, I tested the code with simpler tests such as the Sod test and Sedov blast. I will try. Yes, I am reconstructing density, velocities and pressure, then from the reconstructed pressure I obtain the temperature for the eigenvalues. I must have messed something up because I thought I sent a reply with all the equations, but apparently something went wrong. Tomorrow I'll write it again |
|
|
|

|
|
|
|
|
#6 |
|
New Member
Maksim
Join Date: Jul 2020
Posts: 10
Rep Power: 6  |
||
|
|

|
|
|
|
|
#7 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Could be one of many reasons. With density-pressure reconstruction your temperature is not TVD.
|
|
|
|

|
|
|
|
|
#8 |
|
New Member
Maksim
Join Date: Jul 2020
Posts: 10
Rep Power: 6  |
But from my experience, on contrary, density-velocity-pressure reconstruction instead of density-momentum-total energy allows to avoid negative temperature in some cases, for example Woodward and Collela two blastwave test.
|
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
One important thing you have to consider is that a thermodynamic quantity is uniquely linked to two other thermodynamic quantities. Moreover, you are using a linear interpolation during the TVD reconstruction. You have two choices for the facial values: Either you violate thermodynamic consistency between thermodynamic quantities or you stick to it however, violate the TVD property for all other thermodynamic quantities. This is the price you have to pay for numerical methods higher than first order, see Godunov theorem. It would be helpful to write down the equations, otherwise it is hard to tell you what might be the problem. |
||
|
|

|
||
|
|
|
#10 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
These are the equations:
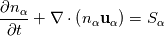 ![\frac{\partial \left(n_\alpha \textbf{u}_\alpha\right)}{\partial t} + \nabla \cdot \left(\left(n_\alpha \textbf{u}_\alpha\right)\textbf{u}_\alpha\right) = \frac{qn_\alpha}{m_\alpha}\left[\textbf{u}_\alpha\times \textbf{B} + \nabla \phi\right] - \frac{1}{m_\alpha}\nabla P_\alpha \frac{\partial \left(n_\alpha \textbf{u}_\alpha\right)}{\partial t} + \nabla \cdot \left(\left(n_\alpha \textbf{u}_\alpha\right)\textbf{u}_\alpha\right) = \frac{qn_\alpha}{m_\alpha}\left[\textbf{u}_\alpha\times \textbf{B} + \nabla \phi\right] - \frac{1}{m_\alpha}\nabla P_\alpha](/Forums/vbLatex/img/57504da0d5591903cb669b961eb68202-1.gif)  which are integrated for electrons and ions where q is the charge (  e, the fundamental charge), B the magnetic field, in my case perpendicular to the domain, e, the fundamental charge), B the magnetic field, in my case perpendicular to the domain, 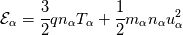 the total energy ( Note that T is expressed in eV here), the total energy ( Note that T is expressed in eV here),  the energy injection source term and the energy injection source term and 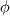 the elctric potential obtained from: the elctric potential obtained from:  At the moment I am trying also with a Strang splitting, so that I solve for the homogeneous system which is identical to Euler. The eigenvalues are the usual eigenvalues. In the algorithm I advance one dt the single species and then compute the new potential for the next timestep. If you are not familiar with plasma, just as a reference, the problem is complicated by the broad range of timescales. For instance, for Xenon m_i = 2.18e-25 kg and m_e = 9.1e-31 kg, so that there is a huge difference in the timescales of ions and electrons. Thermal velocities for electrons are in the order of 1e6 m/s and the temperature is 1-2 order of magnitude larger than the one of ions. Moreover, to solve the non-neutrality of the problem, the debye length and plasma frequency must be resolved, limiting the problem to very fine meshes and timesteps in the 0.5-10 ps order. I know that in the pressure-density-velocity the TVD is not granted, but more in general the positivity of schemes such as the Rusanov is not granted either for multidimensional system with reconstruction > order 1. The negative temperature sometimes occurs in the face reconstruction, but that is easily solvable (or at least more easily with a dedicated limiter), but sometimes it just pops up in the cell centre. After I advance in time the conservative variables, recovering the temperature in the cell centre my give rise to a negative value. Note that in this problem it is not necessary to know the temperature at cell centre, but if one has to compute collision frequencies ecc. it is mandatory. I know that there is a work from Linde and Roe where multidimensional schemes of order >1 are made positive preserving using a dedicated limiter, which however is somehow not straightforward for the pressure. Indeed they state that the pressure must be limited iteratively to guarantee the positivity. I would try to avoid this given the fact that the timestep is already incredibly small and time can be an issue. https://link.springer.com/chapter/10...-011-5169-6_16 By the way, does it make sense for you that i can see a discontinuity in the solution (again in the temperature, but I guess only because I am dividing by the discontinuous density) where I use 1st order rusanov instead of 2nd order HLLEM? Should the interface be smooth? Because I might have an error in the code if that is the case |
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
|
Typically, if the error is in the roundoff, and the code has been properly coded, you can test it by temporarily switching to a higher precision and see if the problem is still there.
|
|
|
|

|
|
|
|
|
#12 |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Yes I tired doing that, but I am already in double precision and MUMPS (the parallel linear solver I am using) does not work with quadruple precision, so in the end I abandoned the test.
|
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
No problem, I am familiar with plasma. Currently I am not quite sure why temperature is explictly needed in your system during time advancement. Your model is closed with a caloric EoS, only. Temperature seems to be needed only for postprocessing. How is pressure connected to internal energy? Via standard thermodnymic relations? Regards |
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
|
Oh, ok... altough, on a second tought, if you already identified the offending line in your code and the reason behind it, there is little to be gained from that. I mean, if legit input then gives you a wrong output on a certain line, you already know what the problem is.
|
|
|
|

|
|
|
|
|
#15 | |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Quote:
You are right that in this particular problem the temperature at cell centre is not used by the code anywhere. Thus I guess the failure mechanism when I see negative temperature in the dataset is: advance one step -> compute temperature for post processing and get T<0 -> at the next computation also the reconstructed temperature at the face is going to be negative and then it fails on c = sqrt(5/3*e*T/m) so yeah eventually I guess it is always the face temperature that makes the code fail. Yes I use standard relations assuming scalar pressure |
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
|
There are simple bechmark shock tube cases that would only work for positivity preserving schemes. Have tou tried your first and second order hllem scheme against those?
|
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
As Paolo already said. It may be useful to check some standard shock-tube examples. Using a TVD reconstruction + special Riemann solvers, often violate some entropy constraints. Regards |
||
|
|

|
||
|
|
|
#18 | |
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Quote:
Isn't obtaining T<0 at cell centre possible because the scheme is not positive preserving? Since my conserved variable which i solve for is the total energy, if the scheme is not positive conservative or the condition for which it is are violated (for instance cfl <0.5 for Rusanov) then I can get T<0. But this is beyond the numerical implementation of the code, but rather an issue due to the linearization of the Riemann problem performed by the approximate solver, correct me if I am wrong. Anyway I tried doing the Noh test, very quickly so I might have an issue with the boundary condition. Since wall condition are not imposed in my code, I solved for all the cylindrical geometry and I put 1st order outflow conditions at the external boundaries (instead of enforcing the analytical solution). With the above system of equation, with the source terms = 0 (exception made for pressure gradient which is part of the flux in my code) : m = 1e15 kg n = 1e-15 m^-3 p = 1e-6 Pa domain 1x1 cm and 800x800 cells max cfl in both directions = 0.1 attached you can see the comparison of Rusanov and HLLEM with 2nd order MUSCL. HLLEM behaves strangely at the origin and in general inside the shock so there might be some issue in the code I guess, but what could that be? Moreover, by looking at the density plot, the square shape originating far from the shock is due to the boundary condition, being a 1st order extrapolation reflects something I guess. In any case after a while the shock collapses in a weird shape, with both schemes ,as reported in one of the picture. Is this normal? I never saw the "long" time solution of the Noh problem. sorry I did not see this, no I did not try them.. I could try the double rarefaction wave and the hurricane-like simulation with vacuum in the centre. I will let you know |
||
|
|

|
||
|
|
|
#19 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
Both of your solutions, Rusanov and HLLEM, look quite oscillatory. My simulations do not contain these little wiggles, even if I use an HLLC instead of a HLLEM. The collapse is due to your boundary conditions and seems ok. Regards |
||
|
|

|
||
|
|
|
#20 | ||
|
New Member
Davide
Join Date: Apr 2023
Posts: 10
Rep Power: 3  |
Quote:
First of all thank you for the reply. I think we are talking about the same thing, for me a positive preserving scheme is a scheme that generates "physically admissible solutions from physical data" [1], or in other words it keeps positive pressure and density if the initial condition are positive. For the Euler equations the physically admissible state in this case is defined as: 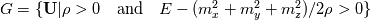 being U the conserved variable vector and m the momentum along the 3 directions. For example Roe scheme is not positive preserving and neither is Osher's. Einfeldt [2] demonstrated that the Rusanov and HLLE are positive preserving, but for example HLLEM is not. All this holds true for 1st order schemes, once 2nd order schemes are taken into account, from what I found there is no proof of satisfying the positive preserving property. That is why the Muscl reconstruction near low density fails also for Rusanov. Clearly if the timestep is strongly reduced this is in general postponed, but inevitable. Having said this, I am new to the study and application of Riemann solvers so I might have said something wrong. Going back to Noh: Quote:
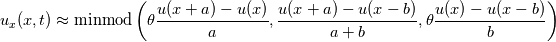 which allows to reduce the diffusivity of the minmod by tuning the parameter ![\theta\in [1,2] \theta\in [1,2]](/Forums/vbLatex/img/6ea7cf4db325a9ed38495334ddd8923e-1.gif) . Setting the parameter to 1 recovers the original minmod. I had it at 1.4. Attached you can find the solution with the parameter = 1. Now the solution is sharp, although the HLLEM keeps behaving strangely at the centre of the domain (note that the simulation is the same, I just cut the plot). Do you have any idea of why it behaves like that at the origin? . Setting the parameter to 1 recovers the original minmod. I had it at 1.4. Attached you can find the solution with the parameter = 1. Now the solution is sharp, although the HLLEM keeps behaving strangely at the centre of the domain (note that the simulation is the same, I just cut the plot). Do you have any idea of why it behaves like that at the origin?Finally, I coded the "hurricane" test described in [4] where a uniform domain is initialized with a vortex like velocity. This creates a vacuum point in the centre of the domain and if the scheme is not positive preserving, eventually it will fail. Of course 2nd order MUSCL Rusanov, HLLE and HLLEM fail in this, but first order HLLE and Rusanov do not. What I did in the end is to use a posteriori approach: I advance 1 timestep, I check for negative pressure, temperature or NANs , If I detect errors, I reject the step and re do it with 1st order Rusanov in the troubled cell and its neighbours. I already tried doing this with little success, but I was not considering the neighbouring cells and just using the Rusanov flux in the troubled one. This eventually does not work. Now I will have to deal with some special cases such as when the troubled cell is on the boundary between processors (I use domain decomposition with MPI). Attached you can see a video of the hurricane like simulation with the HLLEM a polsteriori corrected scheme. Sorry for the low quality, the solution is smooth in reality but the forum has a very low size limit Now I will have to try this on my problem, probably with a careful optimization of the minmod limiter and neighbour radius to avoid failure. [1] https://link.springer.com/chapter/10...-011-5169-6_16 [2] https://www.sciencedirect.com/scienc...21999191902113 [3] https://www.math.umd.edu/~tadmor/pub...or.JCP-00I.pdf [4] https://www.math.hkust.edu.hk/~makxu...D-inviscid.pdf |
|||
|
|

|
|||
 |
| Tags |
| euler, plasma, vacuum |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Solving coupled scalar transport equations in openFoam | pavaninguva | OpenFOAM Running, Solving & CFD | 1 | December 28, 2019 09:28 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 07:27 |
| Riemann invariants of adjoint equations of shallow water equations | zqb0929 | Main CFD Forum | 0 | March 15, 2012 01:54 |
| CFD governing equations | m.gos | Main CFD Forum | 0 | April 30, 2011 15:21 |
| ? fluctuating equations for homogenous shear turb. | ff_fan | Main CFD Forum | 1 | September 20, 2002 08:39 |