 |
|
|
[Sponsors] | |||||
Calculation of Taylor Microscale when Large Eddies are Anisotropic |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
I have a system where the injection of energy is essentially in one dimension. I'm not clear on how to calculate the Taylor microscale. As I understand it, there can be isotropic turbulence on a very small scale even if the large-scale eddies are anisotropic.
The Taylor microscale is given by (taken from wikipedia): 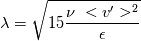 where <v'> is the root mean square of the velocity fluctuations. In general, for velocity fluctuations in three dimensions: 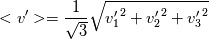 The issue is that the rms velocity for the Taylor microscale is based on the large-scale eddy velocity fluctuations (and not the velocity scale of the Taylor microscale itself). As I understand it, isotropy is often assumed on the large scale so that: 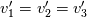 So for isotropic turbulence, equation 1 (first equation in this text) yields: 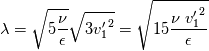 But if, in reality, there is only a fluctuation in one direction for the large scale eddies, how can I calculate the isotropic Taylor microscale? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,747
Rep Power: 66    |
Except in homogeneous turbulence or decaying turbulence where return to isotropy is permitted, fluctuations are rarely exactly equal in each direction. Even kolmogorov scale fluctuations are double in the streamwise direction compared to wall-normal or wall-parallel directions in pipe/channel flows.
The theory you are referencing comes from homogeneous isotropic turbulence where someone has seen the structure function and given you the correlation (i.e. 15). In general, for real turbulence, you plot the two-point correlation functions Rij (Ruu,Ruv,Ruw,Rvv,Rvw,Rww) and that gives you the complete description of what each directional fluctuation is doing at the correlation scale. These are also field functions and depends on where in the flow you are looking. For example, if you look close to the injection point, there are only large eddies and no smaller eddies because the cascade as not taken place yet. And if you look far downstream then you see a more typical cascade. For starters, I recommend you to plot the energy spectrum (or as much of it as you can). From previous posts I am not sure if you are writing a paper or perhaps responding to a reviewer, but something. Is it not sufficient to guestimate the taylor scale length using the longitudinal fluctuations using the formula anyway? If you need that much info about what the fluctuations are doing then you should put in the work and do the analysis and show that at x length scale the rate of production and dissipation are comaparable. If you are just guessing, then just guess. The guessing happens more often than you'd think because even highly accurate measurements of turbulence are done by hot-wire-anemometry where (typically) only the longitudinal fluctuations are measured. You also don't need to do all the work yourself. You could just look in the literature for where someone has already done the measurements and use it and reference it. |
|
|
|

|
|
|
|
|
#3 |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
@LuckyTran:
I have no trouble using the Taylor microscale definition that I showed for isotropic turbulence. In fact, it is a nice upper value for my attempts to extract dissipative microscales from my experimental data. My concern is that someone (a reviewer) or audience participant at a conference might call me out on my definition of the Taylor microscale. I'm wondering if I should call it a Taylor-like microscale or pseudo Taylor microscale or something like that. If I understand you correctly, it sounds like you are suggesting I shouldn't worry about it. My explanation for why I shouldn't worry about it would be that there are many instances where there is not isotropic turbulence on the large-eddy scale, yet researchers still calculate a Taylor microscale using the large eddy velocities. |
|
|
|

|
|
|
|
|
#4 |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
@LuckyTran
As I reread your post, I should note that the system I'm working on is decaying turbulence. In fact, the turbulence is for all practical purposes gone within one large-scale eddy turnover time. Last edited by rdemyan; February 20, 2023 at 19:15. Reason: Additional info |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Forget the expressions for the moment, the question is why a reviewer (or someone else) should ask you for such issue?
You are working on homogeneous isotropic and decaying turbulence, thus the Taylor microscale makes sense for such tasks: - The evaluation of the Reynolds number based on such lenght scale - The evaluation of the Taylor microscale during the decay - The evaluation of the associated Taylor wavelenght in an energy spectra in a DNS simulation Now why are you talking about non-homogeneous flows? |
|
|
|

|
|
|
|
|
#6 | |
|
Member
Join Date: Jan 2023
Posts: 64
Rep Power: 3  |
Quote:
I didn't know that I was talking about non-homogenous flows. At the beginning and end of the energy dissipation zone, I know what the velocities in two of the dimensions are. I know the power injected and I know the size of the energy dissipation zone (one large scale eddy turnover time); thus I can calculate the energy dissipation rate (production equals dissipation). The velocities in the two dimensions are related by a formula. I believe that there is a very small velocity gradient in the third dimension but cannot measure it. As an example, think of a sheet of paper. For the two large dimensions, I know the velocity gradients and they are related. But for the dimension that is the thickness of the sheet of paper (50 microns for a sheet of paper but less in my system), I don't know the velocity gradient. The turbulence has died down after one large scale eddy turnover time because the dimension of the entire system is relatively small (the size of the largest eddies is typically 100 to 300 microns) and I am only studying liquids. So the system is very uniform, but is it homogenous? I would say yes if we are looking at more than one large eddy turnover time. But within one large eddy turnover time there are definitely velocity gradients in space (but the gradients are related and can be calculated). Last edited by rdemyan; February 21, 2023 at 12:17. Reason: Clarification |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
To be honest, I don't understand you. Why the velocity in the third direction should be small? You just talked about decayng turbulence, that means that production is NOT equal to dissipation of energy. The energy is not in statistical equilibrium. Finally, what kind of turbulence are you expecting on 100-300 microns? Homogeneous/isotropic turbulence means specifically that the statistics do not depend on traslation/rotation. What about the information for your system that that happens? |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Dynamic mesh adaption in parallel calculation | xh110120 | FLUENT | 1 | March 12, 2016 09:05 |
| Determining the calculation sequence of the regions in multe regions calculation | peterhess | OpenFOAM Running, Solving & CFD | 4 | March 9, 2016 04:07 |
| MRF and Heat transfer calculation | Susan YU | FLUENT | 0 | June 2, 2010 09:46 |
| Solver and geometry choose for drag coefficient calculation around circular cylinder at large Re | lin | OpenFOAM Running, Solving & CFD | 3 | April 16, 2009 11:50 |
| Warning 097- | AB | Siemens | 6 | November 15, 2004 05:41 |