 |
|
|
[Sponsors] | |||||
Why do we need deferred correction when it can't help yield a valid result? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Deferred correction is often used for higher-order schemes like QUICK, to make the coefficient diagonally dominant. With deferred correction, the solution can converge to the exact solution `x` of the algebraic equations `Ax=b` using the Gauss-Seidel method. Without it, the iterative error may diverge to infinity.
However, the exact solution of `Ax=b` is not necessarily physically realistic. For example, the coefficient matrix A is given by the central differencing scheme when Peclect number > 2. Consequently, what a higher-order scheme using deferred correction may still lead to unphysical solutions. Things are similar when it comes to the QUICK scheme. Hence, I wonder why we need deferred correction. I think convergence to an unphysical solution is no better than divergence of the iterative error to infinity. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
I think you can find the answer of why using deferred correction in many textbooks, for example Ferziger, Peric and Street. On the other hand, numerical oscillations can appear also without using the DC, see for example the convection-diffusion equation with second order central formula at cell Peclet number >2. Your solution is exact in sense of satisfying the discrete equation Ax=b but if you look at the modified differential equation you see that it is a solution of a differential problem having a dispersive term. The fact the a Gauss-Seidel iterative method diverges or not is only a topic to be studied in terms of numerical analysis not in term of physical solution. |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
|
Following your reasoning, every implicit method would be invalid or useless when used in conditions not valid for an equivalent explicit scheme, which is not the case.
Deferred correction is just a way to rearrange terms between implicit and explicit discretizations that, in the end, results in better stability than just using only explicit discretizations. It also has a variety of applications as, in practice, for unstructured grids, it is used for every term that needs higher than 1st order accuracy, including linear problems like just conduction in solids. Note that stretching the time discretization with time steps well beyond the stability of equivalent explicit schemes obviously incurs in time dicretization errors that still make the scheme mostly useless, but for steady state this has no consequences. All in all, the method is also proven with linear problems, where you can verify that indeed you reach the correct solution so, roughly speaking, what you say simply isn't true, at least for linear problems. |
|
|
|

|
|
|
|
|
#4 | ||
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Thanks for your replies, FMDenaro and sbaffini. I just found some useful statements in Hrvoje Jasak's PhD thesis to complement my point:
Quote:
Quote:
But after reading your replies and Jasak's thesis, I'm much clearer now. Now I think DC is just a technique to help converge in the iterative process. Also, I must admit its significance in reducing the size of the computational molecule and changing a pentadiagonal matrix into a tridiagonal one. It's also useful in unstructured grids as sbaffini pointed out. |
|||
|
|

|
|||
|
|
|
#5 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,286
Rep Power: 34   |
Quote:
In modern commerical codes I do not think much of differed correction is used because now the codes are much more stable. |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
|
Quote:
If you instead refer to using a first order central vs a first order upwind for the implicit convective part, I am less sure, yet I have doubts on any advantage. |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
In case of source terms, it is theoretically not correct assuming monotone behavior. The monotonicity is a problem strictly due to the discretization of the convective flux. |
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,286
Rep Power: 34   |
Quote:
I am addressing the part where one says that differed correction produces unphysical results. It can but it does not mean it will always. Your definition about implicit part is correct. This is how it is used in Fluent and starcd. Now a days we just put the higher order values directly to the source, while the matrix (or implicit part) see the contribution from first order scheme. Since we solve in delta form the converged results are not first order results. |
||
|
|

|
||
|
|
|
#9 |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Sorry, I can't understand what "monotonicity" means as to the source terms. Would you please explain it in detail, or just give me some references? Thanks again.
|
|
|
|

|
|
|
|
|
#10 | |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Quote:
|
||
|
|

|
||
|
|
|
#11 | |
|
Senior Member
|
Quote:
It is just the non-delta form that makes things less trivial, but the matter is pretty much the same |
||
|
|

|
||
|
|
|
#12 |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
I introduced an under-relaxation factor into the interpolation formula of the face:
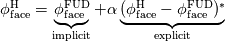 I set different under-relaxation factors: alpha=0.2, 0.5, 0.7 and 1. And test the Central Differencing Scheme with Deferred Correction (CDdc) using one-dimensional cases with different grid Peclect numbers: -0.2, +1, -3, and +10. The RMSE of all cases are listed below. (FUD:First-order Upwind Differencing, PLS:Power Law Scheme) 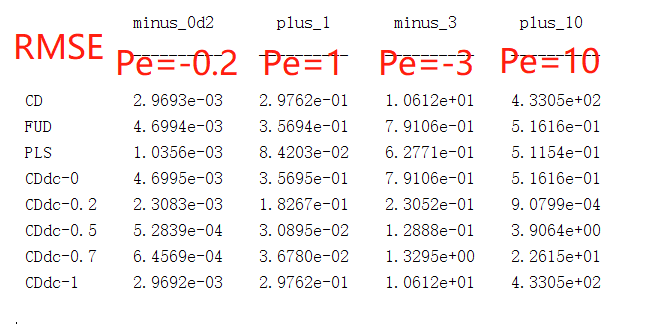 Pe=-0.2 Pe=1 Pe=-3 Pe=10 __________ ________ _______ __________ CD 0.0029693 0.29762 10.612 433.05 FUD 0.0046994 0.35694 0.79106 0.51616 PLS 0.0010356 0.084203 0.62771 0.51154 CDdc-0 0.0046995 0.35695 0.79106 0.51616 CDdc-0.2 0.0023083 0.18267 0.23052 0.00090799 CDdc-0.5 0.00052839 0.030895 0.12888 3.9064 CDdc-0.7 0.00064569 0.03678 1.3295 22.615 CDdc-1 0.0029692 0.29762 10.612 433.05 Obviously, when alpha=1 (0), CDdc-1 (CDdc-0) is reduced to CD (FUD). As you can see, the RMSE of CDdc-1 (CDdc-0) is exactly the same as CD (FUD) regardless of some round-off errors. This also demonstrates that deferred correction cannot help CD obtain bounded solutions at least in these one-dimensional cases. However, when alpha is adjusted to 0.2, 0.5 or 0.7, they could obtain fairly accurate results, and sometimes perform even better than PLS (CDdc-0.2, Pe=10). So I think the DC technique should be used with the relaxation factor to show its significance. (Well, this is called higher order term relaxation in Ansys Fluent Theory Guide.) Last edited by JasmineFeng; February 5, 2023 at 12:06. Reason: Delete an image |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
|
I think there might be something wrong here. DC is not supposed to give an answer when an answer doesn't exist. Nor an answer different from the one expected without DC. It is the same equation with the same discretization, just the terms are rearranged to give certain properties to the matrix.
In your case of linear convection diffusion with central differencing there is an exact numerical solution that should be reached independently from the "time" discretization. Here I highlight time, even if the equation is steady, because there is an aspect that you maybe are not considering. When you solve the linear system without DC you do it in one shot with everything fixed. When you introduce DC you are actually changing the RHS with iterations, so you really solve a different system each time, which is kind of like if you were solving a non linear system in pseudo time. |
|
|
|

|
|
|
|
|
#14 | |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Quote:
|
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
One of the fundamental property of a convection-diffusion PDE is that it does not create new extrema in the solution. Therefore, it is clear that in a numerical solution the presence of new extrema is not physically meaningful. Monotone schemes have a property to guarantee that. But, if a source term is added in the PDE, the action of such a term can actually produce new physical extrema. |
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,882
Rep Power: 73    |
Quote:
I don't understand what you are doing. Negative Peclet means an anti-diffusive problem. Are you just trying to replicate the 1D stready convection-diffusion exercise shown in the textbook of Ferzigr, Peric and Street? |
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#18 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,286
Rep Power: 34   |
Quote:
Try the same problem with Second order upwind, and third order muscl scheme. The problem you have is that you are trying CD. One can apply differed correction for these schemes too like other higher order schemes. What you are finding out is that CD has issues that you think differed correction is introducing them. The CD has peclet problem which is well noted in literature. PS: In other words, you asked for CD solution differed correction provided you CD solution. If you ask for other bounded schemes it will provide you that solution. For example you can use WENO schemes in differed correction way and you will not see problems. |
|
|
|

|
|
|
|
|
#19 | |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Quote:
|
||
|
|

|
||
|
|
|
#20 | |
|
New Member
Jasmine Feng
Join Date: Feb 2023
Posts: 14
Rep Power: 3  |
Quote:
|
||
|
|

|
||
 |
| Tags |
| deferred correction, iterative method |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| error to check simulation result: could not find valid OpenFOAM mesh | xiaoyoyo | OpenFOAM | 5 | May 18, 2017 12:38 |
| [snappyHexMesh] How to define to right point for locationInMesh | Mirage12 | OpenFOAM Meshing & Mesh Conversion | 7 | March 13, 2016 15:07 |
| [snappyHexMesh] determining displacement for added points | CFDnewbie147 | OpenFOAM Meshing & Mesh Conversion | 1 | October 22, 2013 10:53 |
| Timestep and Pressure Correction Relationship in SIMPLE | rks171 | Main CFD Forum | 23 | May 4, 2012 02:04 |
| OF 1.6 | Ubuntu 9.10 (64bit) | GLIBCXX_3.4.11 not found | piprus | OpenFOAM Installation | 22 | February 25, 2010 14:43 |