 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Michael
Join Date: Jan 2022
Location: Birmingham, UK
Posts: 8
Rep Power: 4  |
Dear all, I have some questions about the Smagorinsky model in LES:
(1) In a 2D case, when it is in a corner near walls on both x&y directions, what should be the length scale? (I think it should be the smaller one, but I might have seen some codes in which it multiplies x&y length scales.) (2) If it is near a slip boundary, rather than a non-slip wall, what should the length scale be? The Van Driest damping is 1-exp(-yplus/Aplus) I always regard yplus as a concept near non-slip wall as it involves shear stress. Is there still yplus near slip boundary? What should be Van Driest damping if it is near a slip boundary? Thank you |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
LES is for 3d, not for 2D flows. However, you are considering wall bounded turbulence and you have to know that the concept of filtering applies for homogeneous flow directions. Along the normal to wall direction you cannot thing about a unique characteristic lenght scale, that is the basic topic in turbulence. The Smagorinsky lenght scale is a function of the distance from the wall. But be aware that if you want to set physical BCs at the walls, you have to use a DNS-like grid in the BL. That is no filtering in the vertical direction. |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
|
It's always the nearest wall. By definition, a slip boundary is not a wall.
However, we are talking here about a model, how it was formulated and later refined. Can we esclude that a slip wall would, inviscidly, block eddies of a certain size and thus be relevant for a damping in the Smagorinsky model? No, of course, but the original damping has a very specific origin: fix the wrong near wall behavior of the resulting eddy viscosity and recover the correct 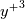 one. It is in this sense, and only this one, that you need to look at the Van Driest correction. one. It is in this sense, and only this one, that you need to look at the Van Driest correction.Which, again, doesn't mean that the VD correction can't be improved for more general flows, but that's another story and I don't know of any serious attempt at it. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Michael
Join Date: Jan 2022
Location: Birmingham, UK
Posts: 8
Rep Power: 4  |
Quote:
Sorry I still don't get it. what is 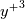 ? Why is it cubic? In the VD damping it's just ? Why is it cubic? In the VD damping it's just  . .
|
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
|
Quote:
Roughly speaking, the Smagorinsky model is there as a surrogate of a turbulent term that, near walls, behaves in a certain way (i.e., 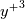 ). But it fails to do so (it is constant instead). That's why it is multiplied by a damping term, to recover that very near wall behavior. ). But it fails to do so (it is constant instead). That's why it is multiplied by a damping term, to recover that very near wall behavior.Unfortunately, not all the damping terms have been formulated correctly or, at least, there is a lot of confusion on their use and the respective models where they are suitable. So, you might have a damping term that goes to 0 at walls (which is better than nothing), yet it fails to do so with the correct slope. Also, sometimes the correct near wall behavior is not really useful, while a different one works better in practice. But the underlying theory is still one, the term that one seeks to model actually goes to 0 at walls as 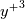 . This, in turn, follows from the fact that the term is u'v', with u' going to 0 as . This, in turn, follows from the fact that the term is u'v', with u' going to 0 as  and v' going to 0 as and v' going to 0 as  (because of continuity and wall parallel velocity gradients being 0 at walls, the wall normal velocity gradient must be 0 as well, meaning that the v' taylor expansion at walls starts with 2nd order terms) (because of continuity and wall parallel velocity gradients being 0 at walls, the wall normal velocity gradient must be 0 as well, meaning that the v' taylor expansion at walls starts with 2nd order terms)
|
||
|
|

|
||
 |
| Tags |
| smagorinsky model, van driest damping |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Cannot calculate Spalart-Allmaras model turbulence length scales? | spalartallmaras | Main CFD Forum | 6 | August 29, 2024 12:20 |
| [swak4Foam] swakExpression not writing to log | alexfells | OpenFOAM Community Contributions | 3 | March 16, 2020 19:19 |
| Turbulence length scale and integral length scale | rizhang | CFX | 2 | April 22, 2016 08:22 |
| Integral Length Scale vs Turbulent Length Scale | Scott Nordsen | FLUENT | 2 | January 20, 2014 02:17 |
| Turbulent Boundary condition, viscosity ratio and length scale | Bollonga | FLUENT | 80 | February 16, 2013 13:06 |