Hi
I'm struggling to understand how a a correct neumann bc for the pressure is supposed to be derived when the Euler equations are used, and moving boundaries are permitted. The impermeability condition reads
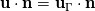
, where
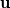
is the flow velocity,
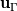
is the velocity of the solid boundary, and
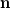
is the normal vector pointing out of the solid domain. The momentum equation projected in the normal direction gives
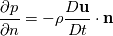
, so the challenge is to find
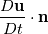
. I've seen a paper with the name of "A high order moving boundary treatment for compressible inviscid flows" take the material derivative of the impermeability condition stated above, which by application of the product rule gives
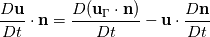
. A source of confusion in the mentioned paper was that the term
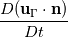
was written as
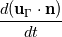
.
I guess my primary issue is to find out how the material derivative of the normal velocity
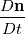
and the term
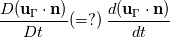
are computed. I'm confused on whether for instance the material normal vector should be "advected with the flow" or if it's described relative to the solid body. In the case of a curved, static boundary
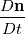
would yield a nonzero term for a nonzero tangential velocity, while
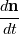
would yield zero anyway, if I'm not mistaken.
If someone could explain or possibly point me to a nice source on the topic, it would be greatly appreciated.



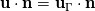 , where
, where 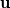 is the flow velocity,
is the flow velocity, 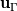 is the velocity of the solid boundary, and
is the velocity of the solid boundary, and 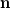 is the normal vector pointing out of the solid domain. The momentum equation projected in the normal direction gives
is the normal vector pointing out of the solid domain. The momentum equation projected in the normal direction gives 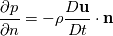 , so the challenge is to find
, so the challenge is to find 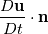 . I've seen a paper with the name of "A high order moving boundary treatment for compressible inviscid flows" take the material derivative of the impermeability condition stated above, which by application of the product rule gives
. I've seen a paper with the name of "A high order moving boundary treatment for compressible inviscid flows" take the material derivative of the impermeability condition stated above, which by application of the product rule gives 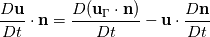 . A source of confusion in the mentioned paper was that the term
. A source of confusion in the mentioned paper was that the term 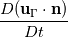 was written as
was written as 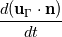 .
. 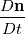 and the term
and the term 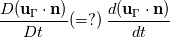 are computed. I'm confused on whether for instance the material normal vector should be "advected with the flow" or if it's described relative to the solid body. In the case of a curved, static boundary
are computed. I'm confused on whether for instance the material normal vector should be "advected with the flow" or if it's described relative to the solid body. In the case of a curved, static boundary 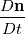 would yield a nonzero term for a nonzero tangential velocity, while
would yield a nonzero term for a nonzero tangential velocity, while 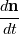 would yield zero anyway, if I'm not mistaken.
would yield zero anyway, if I'm not mistaken.

 Similar Threads
Similar Threads