 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
In your problem you used the Prandtl equations, that is parabolic x-component momentum equation (x is a time-like direction) coupled with the hyperbolic divergence-free equation.
You need to start from the BC at x=0 (trailing edge) and integrate the equations, for each position x, along the y direction. But that must be done only in the interior nodes. At x=L (last position) the velocity profile is computed as same as for the previous nodes, indeed your flat plate extends up to x->Inf. You have to study the integration for a parabolic equation like the heat equation (but in your case the equation is not linear) but also to be aware how to manage the divergence-free constraint. |
|
|
|

|
|
|
|
|
#22 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
Yes it is nonlinear but I am, for example, using u(i,j,k)*u(i,j,k-1) to linearize it in the momentum equation. Any guidance is welcome/appreciated. |
||
|
|

|
||
|
|
|
#23 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Is there a reason you're trying to use a backward difference scheme in the y-direction? That's a very poor choice. Just use central differencing.
Or is that the purpose of this exercise? If you still want to do backward diffferencing then it is: 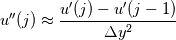 And you need to retrieve u' on the wall. Now it becomes a question of how do you choose to evaluate the gradient du/dy? Also backward or...? |
|
|
|

|
|
|
|
|
#24 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
You have a 3D case? Write here the discretization of the full system of equations |
||
|
|

|
||
|
|
|
#25 |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
|
|
|
|

|
|
|
|
|
#26 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
inner nodes continuity: u(i+1)-u(i-1)/(2*delx)+ v(i,j+1)-v(i,j-1)/(2*dely) = 0 inner nodes momentum: u(i,j)(u(i+1)-u(i-1)/(2*delx) + v(i,j) (v(i,j+1)-v(i,j-1)/dely =mu/rho * (u(i,j-1)-2*u(i,j)+u(i,j+1))/dely^2 For outlet: v(i,j)=v(i,j-1)-dely/delx (u(i,j)-u(i-1,j)) and using momentum equation u(i,j)(u(i,j)-u(i-1))/delx + v(i,j)(u(i,j)-u(i,j-1))/dely = mu/rho* ( u(i,j-2) -2*u(i,j-1) +u(i,j))/dely^2 |
||
|
|

|
||
|
|
|
#27 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
If i apply central differencing, then wouldnt I be using inconsistent schemes in the momentum equation? like for example, in first term u velocity is out of the outlet to the right. How to address that ? or should backward diff work here in the same equation. |
||
|
|

|
||
|
|
|
#28 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
There is no d2u/dy2 in the continuity equation... What is inconsistent with what?
You most likely have the Neumann condition at the outlet: d(anything)/dx=0. That's why you just duplicate the values from the interior node onto the outlet node. I'll say it again, there is no governing equation on a boundary node. Only boundary conditions.... Stop asking how and stop trying to discretize the governing equation at the outlet.... Even if you don't have a Neumann condition but some rather complex outlet BC, then you get the values per whatever is the BC. For example... How do you determine the velocity at the inlet nodes? You use the boundary conditions. How do you determine the velocity at the upper boundary? It's U infinity. The boundary condition. How do you determine the velocity at the wall nodes? It's zero because of no-slip. No governing equation involved. Only boundary conditions. |
|
|
|

|
|
|
|
|
#29 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
First, do you use staggered or colocated arrangement?
Then there is no physical outlet in the flat plate theory, the length of the plate is infinite. You just have a computational finite domain but the theory of the characteristic says you cannot prescribe a velocity but it is a result fo the computation of the equations. |
|
|
|

|
|
|
|
|
#30 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
|
||
|
|

|
||
|
|
|
#31 |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
There is no neumann condition on the outlet.
|
|
|
|

|
|
|
|
|
#32 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
|
||
|
|

|
||
|
|
|
#33 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
There is a boundary condition at the outlet, you just don't realize it yet.
I'm suggesting that it is a Neumann condition based on the fact that you haven't realized it yet, but it could be something more complicated like a characteristic BC or a non-reflecting BC or... lots of things. But it's not a governing equation. A boundary value problem is not defined until you have specified boundary conditions on ALL boundaries. |
|
|
|

|
|
|
|
|
#34 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
How do you compute the velocity at the node just before the "outlet" section? Repeat the procedure. You have an equation like u(i+1,j)=u(i,j) + F(u,v) See Sec.3.3 https://essay.utwente.nl/63314/1/BSc...Puttkammer.pdf |
||
|
|

|
||
|
|
|
#35 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
|
||
|
|

|
||
|
|
|
#36 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Actually, no, there is no BC you can prescribe due to the parabolic/hyperbolic character of the equations: the domain of integration is open. The profile is determined by integrating the equation at every station x since the flat plate is infinite. |
||
|
|

|
||
|
|
|
#37 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Quote:
Actually, I agree. If this is indeed an infinite flat plate (and it should be since this is the Prandtl equation), it means the domain of integration is open on the right and there is no physical outlet and no need to discuss boundary nodes at the outlet. Then the calculation procedure for the right most cell is same as the procedure for the one just before it, recursively so. |
||
|
|

|
||
|
|
|
#38 | |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
Quote:
 very useful document. thanx very useful document. thanx
|
||
|
|

|
||
|
|
|
#39 |
|
Member
Shah
Join Date: Aug 2013
Posts: 61
Rep Power: 13  |
For the convective term in steady equation, is it correct to write:
u du/dx = u(i,j)* (u(i,j)-u(i-1,j))/delx ? I am of the view that it is nonlinear. How should one proceed? Should one change the scheme? any guidance please. |
|
|
|

|
|
|
|
|
#40 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
This is a first order upwind scheme, the backward derivative is correct for positive u, as is in your case. |
||
|
|

|
||
 |
| Tags |
| backward differencing, finite difference, rectangular domain |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| On the diffusion term discretization on unstructured grids | sbaffini | Main CFD Forum | 33 | November 10, 2017 04:20 |
| Why in Hrvoje Jasak's thesis diffusion term has "rho"? | cavida | OpenFOAM Programming & Development | 6 | February 4, 2016 08:10 |
| Discretization of the Diffusion Term | Rui | CFX | 0 | October 24, 2005 13:43 |
| Source term for diffusion equation in FLUENT 4.5 | Raja Banerjee | FLUENT | 1 | August 31, 2000 00:00 |
| Numerical diffusion error | Z.Zeng | Main CFD Forum | 8 | October 22, 1999 10:06 |