 |
|
|
[Sponsors] | |||||
Navier-Stokes equation in spherical coordinate |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Hi All,
I need to solve Navier-Stokes equation in spherical coordinate. Prof. Batchelor gave mass and momentum equations directly without derivation in his book "An introduction to Fluid Mechanics", 1967. Besides, some show a coordinate transformation from Cartesian, which is not clear from a physical basis. So I want a complete derivation from basic conservation laws. Could someone help? Thank you so much. Best, Mingming |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 376
Rep Power: 11  |
Dear Mingming:
If you are looking for a direct transformation between the Cartesian equations to the spherical coordinates, look up something called "Lamé coefficients." This should simplify your work. Otherwise, if you are looking for a direct derivation of these equations in spherical coordinates, you might want to start with mass conservation (continuity) and try to derive it yourself and then infer (not repeat) this for the momentum equations. Hope that helps, Gerry. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
That means you want to write the Reynolds transport equation in spherical coordinates and then mass, momentum and energy? |
||
|
|

|
||
|
|
|
#4 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
Yes, I derived continuity equation by myself from mass conservation, but failed for the momentum equations. There must be something missing that I have to dig into. Thank you so much. Best, Mingming |
||
|
|

|
||
|
|
|
#5 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
Yes, mass, momentum, energy and chemical species conservation equations for incompressible flows. I have derived them from scratch in Cartesian coordinate, with porous media included. But spherical coordinate is quite different. Could you please give me some hint? Thanks, Mingming |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
The NSE in spherical coordinates are detailed in many textbooks. I suggest to start from the simple polar representation (without porous effects) to check if you are doing correctly your derivation. You need to express the nabla and integral operators in sperical coordinates and then apply the inner product to the momentum variable. Maybe you could write the point in which your derivation failed. |
||
|
|

|
||
|
|
|
#7 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
I probably missed unit vectors relationship but I can not tell exactly. Yes, I tried cylindrical coordinate without porous media but not complete yet. BTW, would you please name a book which has a complete derivation? Thank you. Best, Mingming |
||
|
|

|
||
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
post your notes and we can check .... Have a look to the dedicated appendix in the textbook of Kundu. |
||
|
|

|
||
|
|
|
#9 |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
||
|
|

|
|
|
|
|
#10 |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 376
Rep Power: 11  |
I remember this being in my course notes from some decades ago. The direct derivation of the momentum equations in the spherical coordinates are not so straightforward.
What you can do, is to assume a set of transformation coefficients (i.e., Lamé coefficients). Leave them "as is" (i.e., as h1, h2, and h3) until the very end, since you are deriving differential equations. These coefficients are conservative so the advantage is that you simply have to carry them in your derivation and then substitute them when you have the governing equations in basic form, effectively treating the derivation as Cartesian for the most part. I imagine this is also the same approach as what is shown in Batchelor's text. What these coefficients are you can infer from the continuity equation, which you have already done. Also, how are you modelling porous media? With Darcy / Forchheimer relations, or explicitly (i.e., porous interface as walls)? Gerry. |
|
|
|

|
|
|
|
|
#11 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
Thanks for your suggestions. I use Darcy's law to model resistence of porous media. Best, Mingming |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
Gerry Kan
Join Date: May 2016
Posts: 376
Rep Power: 11  |
Quote:
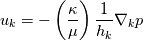 where  is the permeability, is the permeability, 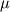 is the dynamic viscosity, is the dynamic viscosity, 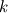 is the individual orthogonal component is the individual orthogonal component 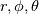 , and , and 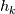 are the Lamé coefficients for each of the component. are the Lamé coefficients for each of the component. What you will have should be: 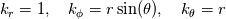 . .If you need to be convinced for the spherical coordinates, you can derive the Lamé coefficients from mass conservation alone. The corresponding differentials (  ) and substitute this into your momentum equations to save you work in deriving everything, since it will get very messy for spherical coordinates. ) and substitute this into your momentum equations to save you work in deriving everything, since it will get very messy for spherical coordinates.Gerry. |
||
|
|

|
||
|
|
|
#13 |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
It seems that spherical coordinate is not friendly. I'll keep this in mind. Thank you so much. Best, Mingming |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,762
Rep Power: 66    |
In my opinion, this is best done by deriving the vector form of the Navier-Stokes equations using divergence operators (this is also the meta). Then you can freely go into any coordinate system you want. Coordinates are just representations of vectors, the underlying physics remains the same.
|
|
|
|

|
|
|
|
|
#15 |
|
New Member
cartlon flores
Join Date: Feb 2022
Posts: 1
Rep Power: 0  |
I derived continuity equation by myself from mass conservation, but failed for the momentum equations. shareit downloading vidmate 2014
Last edited by sonmezroy; February 26, 2022 at 05:09. |
|
|
|

|
|
|
|
|
#16 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
I followed your suggestion and succeeded. At this moment, only mass and momentum equations are derived without porous media, species and energy equations are the next step. Thank you very much. Best, Mingming |
||
|
|

|
||
|
|
|
#17 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
How did you work out mass conservation equation? I'd like to share my notes but it's not in English. You can email me at zmmhst0819@gmail.com. Best, Mingming |
||
|
|

|
||
|
|
|
#18 |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Dear CFDers,
I have derived mass and momentum equations in sperical coordinates by hand, to have a deeper understanding of variables in spherical coordiantes. Anyone interested in could contact me at zmmhst0819@gmail.com. Cheers, Mingming |
|
|
|

|
|
|
|
|
#19 | |
|
Member
Mingming Zhang
Join Date: Dec 2019
Posts: 35
Rep Power: 7  |
Quote:
I recently found a paper that uses finite difference method to solve NS equations in spherical coordinates. It provides an interesting pseudo-velocity method to circumvent singularity problem. It's "A fi nite difference scheme for three-dimensional incompressible fows in spherical coordinates" by Luca Santelli. Best, Mingming |
||
|
|

|
||
|
|
|
#20 |
|
New Member
Uno
Join Date: Jul 2022
Posts: 1
Rep Power: 0  |
Yes, I derived continuity equation by myself from mass conservation, but failed for the momentum equations. There must be something missing that I have to dig into.
__________________
UNO blank card rules |
|
|
|

|
|
 |
| Tags |
| ns equation, spherical coordinate |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Line term in the Navier - Stokes equation. | vgoy | OpenFOAM Programming & Development | 2 | October 26, 2021 10:07 |
| Navier Stokes Equation for Non-newtonian fluid? | shivasluzz | Main CFD Forum | 6 | June 9, 2015 11:44 |
| need 2d equation for navier stokes in c | sudeep | FLUENT | 1 | February 16, 2011 18:01 |
| Navier stokes compresible viscid flow fea, somebody can help? | Jose Choy | Main CFD Forum | 3 | October 24, 2003 03:28 |
| help: I am trying to solve Navier Stokes compressible and viscid flow | Jose Choy | Main CFD Forum | 2 | May 18, 2000 06:45 |