 |
|
|
[Sponsors] | |||||
Correlation, energy spectrum and integral length scale |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
In homogeneous isotropic turbulence (HIT), the correlation function
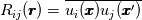 and the energy spectrum tensor 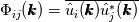 are a Fourier-transform pair, i.e., 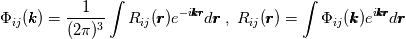 where 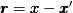 , , 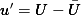 is the fluctuating part, and is the fluctuating part, and 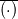 represents the averaging. Additionally, the longitudinal integral length scale is defined as represents the averaging. Additionally, the longitudinal integral length scale is defined as 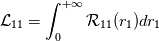 where 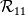 is the correlation coefficient in the longitudinal direction. is the correlation coefficient in the longitudinal direction.Combine all these, one can derive the integral length scale from the one-dimensional spectrum 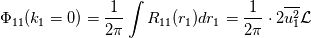 thus giving 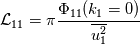 However, for HIT, 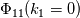 is expected to be zero, given that the zeroth mode is expected to be zero, given that the zeroth mode 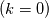 for velocity should be zero mean. Hence, from above, the integral length scale will be zero as well. This doesn't seem right to me. So could anybody point out where am I missing? for velocity should be zero mean. Hence, from above, the integral length scale will be zero as well. This doesn't seem right to me. So could anybody point out where am I missing?Thanks. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Your case represents a full periodic box, in such a case the characteristic scales is the Taylor microscale. Clearly, while considering only fluctuations, there is no meaning in a characteristic lenght scale for the “large” structures.
|
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
|
Quote:
![[0,2\pi] [0,2\pi]](/Forums/vbLatex/img/1cc5fb6d3b10cf0b4029e23d46fa7fc0-1.gif) brown.jpeg Clearly, it is long-range correlated, and we can extend the concept above and define an integral length scale for this signal. However, from the math I showed, the integral length scale is determined by the mean (i.e., the 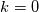 mode), which will be zero in this case. This still doesn't make sense. mode), which will be zero in this case. This still doesn't make sense.
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
In isotropic homogeneous turbulence, the integral length scale
 is defined as the weighted average of the inverse wavenumber, i.e., is defined as the weighted average of the inverse wavenumber, i.e.,  where  is the energy spectrum. is the energy spectrum. Have also a look to this paper https://www.researchgate.net/publica...Numerical_Data |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
The velocity fluctuation signal u' has zero Fourier coefficient.
The energy spectrum is the Fourier transform of the correlation function (more technically the two-point correlation function) which is non-zero if there is any correlation. And as you say, clearly it is (long-range) correlated. Unless the signal is a trivial (zero everywhere all the time) then it will almost certainly have a finite correlation. |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
|
Quote:
Same result is shown in Eq.4.11 in here, even though it's in time. |
||
|
|

|
||
|
|
|
#7 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
If you subtract the DC part of a signal (or use any signal with zero mean), you get that the energy spectrum is 0 corresponding to a mean of 0. It says nothing about the length scale.
That is, phi is zero and u bar is zero. Any length scale satisfies that. |
|
|
|

|
|
|
|
|
#9 | |
|
Senior Member
|
Quote:
Take the 1-D signal I mentioned in one of the reply above for example. It's a periodic signal with zero mean, and clearly, 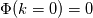 . By extending the derivation above, . By extending the derivation above, 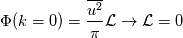
|
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Something in your formula makes me think about an ideal case: imagine a total random signal, that is a white spectrum. It is uncorrelated, you will see the separation point ->0. And the formula seems to become an identity like 0=0*0 ...But, on the other hand, a small correlation would produce the RHS to be non vanishing. |
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
If your signal has zero mean then u bar is zero.
 And phi is zero like you say. This does not imply that L is zero. If you re-arrange the formula for L then you make the division by 0 mistake.  I think what you are forgetting is that u bar is zero. |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Well, be careful, his formula has (u^2)_bar= (u'^2)_bar. |
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Let me just take a step back and ask from where do we get
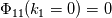 And what kinds of signals are we talking about? Their properties cannot be ignored. White noise is uncorrelated. Brown noise has a flat non-zero power spectral density. Arbitrary but otherwise statistically stationary signals have correlation. |
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
|
Quote:
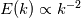 , not a flat one; flat one is for white noise. , not a flat one; flat one is for white noise.
|
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
|
Quote:
 , the , the  here is the fluctuating part, i.e., here is the fluctuating part, i.e., 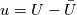 , as I already indicated in the post; indeed, , as I already indicated in the post; indeed, 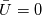 . Anyway, I don't think the denominator will be zero. . Anyway, I don't think the denominator will be zero.And for why 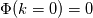 . Recall that I consider a 1-D zero-mean brown noise above, and in 1-D the energy spectrum is . Recall that I consider a 1-D zero-mean brown noise above, and in 1-D the energy spectrum is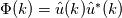 in which  is the Fourier transform of the fluctuating part is the Fourier transform of the fluctuating part 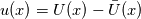 . Since the noise is zero mean, . Since the noise is zero mean, 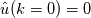 , and so , and so 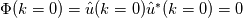 . .
|
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
You're right. Brown noise is the integral of white noise. The power spectral density for white noise is a constant. The power spectrum for brown noise goes like 1/f^2 or 1/k^2 since we're talking about space. Either way, neither are identically zero.
The Fourier transform of a constant is not 0. |
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
|
Quote:
For a zero-mean signal, isn't the zeroth-mode (or the DC component) 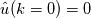 ? Then the spectrum ? Then the spectrum 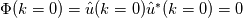 ? ?
|
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
You're probably thinking that
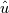 is the thingy you see when you plot an FFT or the amplitude when you look at a Fourier plot. That's only the real part of the complex Fourier representation. There is also an imaginary part. is the thingy you see when you plot an FFT or the amplitude when you look at a Fourier plot. That's only the real part of the complex Fourier representation. There is also an imaginary part.If consider a constant signal with non-zero mean, a simple DC signal, the Fourier transform of a constant DC signal is a Dirac delta function. The special case of the constant being 0 has very peculiar properties. Basically, 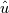 ain't 0. ain't 0.
|
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
|
Quote:
|
|
|
|

|
|
 |
| Tags |
| correlation, integral length scale, velocity spectrum |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| help Energy spectrum 2.0 | bhigahAshish | Main CFD Forum | 7 | July 14, 2019 06:20 |
| Energy spectrum in frequency | bhigahAshish | Main CFD Forum | 4 | July 7, 2019 11:54 |
| From the correlation tensor Rii to the three-dimensional spectrum E(k). | lucamirtanini | Main CFD Forum | 4 | January 30, 2019 12:28 |
| Integral Length Scale - 2D | WhiteShadow | Main CFD Forum | 5 | May 19, 2018 17:56 |
| von Karman curve fitting to field measured spectrum | doutormanel | Main CFD Forum | 0 | October 18, 2012 10:02 |