 |
|
|
[Sponsors] | |||||
Correlation, energy spectrum and integral length scale |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#22 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#23 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Yes an no. I only want to indicate that the first thing you assume is that the first mode should zero
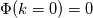 . The logical order then says that physical squared (mean) signal has to be zero . The logical order then says that physical squared (mean) signal has to be zero  . This may imply (or not) in a second step that the mean signal has also to be zero . This may imply (or not) in a second step that the mean signal has also to be zero  . And in a third step this is linked with the length scale . And in a third step this is linked with the length scale 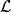 . .I think the logical order is import here. It should be clearly defined what is assumed and what is the derived. |
|
|
|

|
|
|
|
|
#24 |
|
Senior Member
|
Quote:
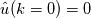 , then 2. in 1-D, we can get rid of the averaging and get , then 2. in 1-D, we can get rid of the averaging and get 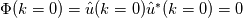 . .
|
|
|
|

|
|
|
|
|
#25 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
 is u(t) in Fourier space. is u(t) in Fourier space.You can write u(t) as a summation of its bases (you are doing the same thing when you claim that u hat is 0 btw). I say that it is a constant function just to help illustrate the point (zero-mean is a constant w/ value of zero). To appreciate where the Dirac delta comes from, it's easier to do in complex space. Real-valued signals have complex Fourier representations. The Fourier transform is real only for even functions. Cosines and sines also have zero mean. Their Fourier transforms are not identically zero and their Power spectrum are not identically zero. Take cos(a*t) for example, and take the limit as a approaches 0. Just simply being zero-mean isn't enough. |
|
|
|

|
|
|
|
|
#26 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
I would also say that just zero mean is not enough.
Think of a zero mean signal made of positive and negative random values (or Cosines and sines). What does happen if you square these values? You are not allowed to skip the multiplication under the average bar before you apply the modal transformation. The order of the operations is important. |
|
|
|

|
|
|
|
|
#27 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
If we use a sin x function in 0;2pi we have a signal with zero mean. The Fourier trasform has only the spike at k=1 and all other coeffients are zero.
Does that means we have also a vanishing integral lenght? Take the autocorrelation and see. |
|
|
|

|
|
|
|
|
#28 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Some links that could be useful
https://ntrs.nasa.gov/api/citations/...0150000733.pdf https://www.io-warnemuende.de/tl_fil...Chap4_WS08.pdf |
|
|
|

|
|
|
|
|
#29 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#30 | |
|
Senior Member
|
Quote:
![k\in[0,100] k\in[0,100]](/Forums/vbLatex/img/4047f1341a8cfcbb5bf02f89fe93a490-1.gif) ) and average. ) and average. Though this is somewhat strange to me. I don't understand the meaning behind this. |
||
|
|

|
||
|
|
|
#31 | |
|
Senior Member
|
Quote:
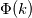 , I don't see how we can apply the averaging, since there is only one wavenumber component, and there are no spherical shells. , I don't see how we can apply the averaging, since there is only one wavenumber component, and there are no spherical shells.
|
||
|
|

|
||
|
|
|
#32 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
for you Int[0 : pi] cos x dx = 0 ??????     :con fused: :con fused:
|
||
|
|

|
||
|
|
|
#33 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Quote:
Order of operations is important. You need to take the Fourier transform as a function of all wavenumbers and square it. Then take the average. And then put k=0 to find the power spectrum at k=0. If f(x) = x and I ask you for the derivative of f(x) at x=0. You wouldn't take f(0) = 0 and take the derivative of 0. You evaluate the derivative as a function of x first f'(x) = 1 and then evaluate f'(x=0)=1. The shells are not important. In 1D you have the simple integrals. In 3D you have spherical shells over the wavevector space. You don't have to worry about that in 1D. But you do need to do the correct averaging (the correct integral). The biggest difference between 1D and 3D is the scaling factor of 2pi is different for 3D. |
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
|
Quote:
Code:
u = colornoise(N); % some external function generates a correlated/colored noise u = u - mean(u); % make sure the mean is zero uhat = fft(u)/N; Phi = uhat.*conj(uhat); Am I correct? |
||
|
|

|
||
|
|
|
#36 | |
|
Senior Member
|
Quote:
Code:
u = colornoise(N); % get a correlated/colored Gaussian noise from a user-defined function u = u - mean(u); % make sure the mean is zero uhat = fft(u)/N; Phi = uhat.*conj(uhat); Am I correct? |
||
|
|

|
||
|
|
|
#37 |
|
Member
EM
Join Date: Sep 2019
Posts: 59
Rep Power: 7  |
||
|
|

|
|
|
|
|
#38 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#39 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Once you have the auto-correlation you need to integrate it from 0 to infinity to get the integral length/time scale. Here you need to be very careful because the integral of sin(x) and cos(x) at infinity is tricky. But if you integrate sin(x) from 0 to infinity you get 1. And if you integrate cos(x) from 0 to infinity, you get 0.
|
|
|
|

|
|
|
|
|
#40 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
There are 3 things going on:
1) The most important one. We have that the integral length/time-scale is defined as the integral of the autocorrelation from 0 to infinity. The signal in question does not even have to have a Fourier transform. Since turbulence is random and non-periodic, this definition works really well. How do we even measure a signal for infinite time? Who knows... It's important to note that turbulent signals have rapidly decaying correlations where the difference between the integral from 0 to t and the integral from 0 to infinity can be small. 2) We have from the Wiener-Khinchin theorem that that the Energy spectrum can be defined as the Fourier transform of the autocorrelation function. We further have the result that the energy spectrum at zero frequency is proportional to the integral scale defined in (1). But this result depends on these things being transformable in the first place. 3) Finally we have Parseval's theorem which gives that the integral of the square of a function is equal to the integral of the square of its Fourier series. That is, the energy is the same if you integrate in spacetime or in spectral spaces. The integral of the signal squared is of course the total power. Hence, the integral of the Fourier transform squared should also be the total power. It is common to define the energy density as the integrand of the energy density at a frequency f is equal to the square of its Fourier component by using a sifting function (i.e. a Dirac-delta function). However, now you have an issue where the PSD defined this way sometimes does not match the PSD defined in (2) as explained. There is a cute example shown in Equations (7) and (8). See also the very last paragraph in Wiener-Kinchin theorem. You have to keep in mind that Parseval's theorem relates the total integral to total integral (Power to Power) and is not actually a statement about spectral density. The underlying issue is that turbulence is continuous, non-periodic, infinite time, and random. Practical data is time-limited. When you take correlations and Fourier transforms of real data, you are doing operations on their periodic extensions. So even if you take real data of a turbulent flow, the thingy that you take the fft of is its infinite periodic extension, which is periodic! You have to be cognizant of the properties of infinite time transforms, windowing, and the relationship between to go back-n-forth between them. If you have a finite-length signal, you can never get the the 0 frequency spectrum in the classical sense. You haven't sampled the signal for infinite time, so how can you have any information about what happens at 0 frequency? What you are doing when you take the fft of real data is performing the Fourier transform on the periodic extension of that signal. This is why it's so important to detrend your data before you do an fft and also why people extrapolate the power spectrum to 0 frequency and don't just take the value at the 0 Hz bin. For turbulent signals the extrapolation makes sense because the spectrum of turbulence is continuous. For arbitrary (e.g. periodic signals), this extrapolation can be absurd. To make a long story short, you have to be careful when you have Dirac delta functions. You should stick to integrating the correlation function unless you can find reversible transformations between the autocorrelation and the PSD. |
|
|
|

|
|
 |
| Tags |
| correlation, integral length scale, velocity spectrum |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| help Energy spectrum 2.0 | bhigahAshish | Main CFD Forum | 7 | July 14, 2019 06:20 |
| Energy spectrum in frequency | bhigahAshish | Main CFD Forum | 4 | July 7, 2019 11:54 |
| From the correlation tensor Rii to the three-dimensional spectrum E(k). | lucamirtanini | Main CFD Forum | 4 | January 30, 2019 12:28 |
| Integral Length Scale - 2D | WhiteShadow | Main CFD Forum | 5 | May 19, 2018 17:56 |
| von Karman curve fitting to field measured spectrum | doutormanel | Main CFD Forum | 0 | October 18, 2012 10:02 |