 |
|
|
[Sponsors] | |||||
Eddy diffusivity and the simple gradient diffusion hypothesis |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
BM
Join Date: Sep 2021
Posts: 35
Rep Power: 5  |
Hi all, newcomer here, and I just hoping of finding some answers on this forum.
My question is regarding the eddy diffusivity and how it is used in the gradient diffusion model and the TKE transport equation. I scoured several websites, textbooks, and papers over the past week, but could not get any clarification on my questions. I'm still relatively new to fluid mechanics, so please correct me if my understanding is completely wrong. Context My understanding is that the eddy diffusivity  describes how some substance is mixed by turbulent eddies within a flow field. There is a mass eddy diffusivity describes how some substance is mixed by turbulent eddies within a flow field. There is a mass eddy diffusivity  , momentum eddy diffusivity , momentum eddy diffusivity 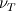 , and heat transfer eddy diffusivity , and heat transfer eddy diffusivity  . These are generally not equal (unless the Reynolds analogy is assumed). . These are generally not equal (unless the Reynolds analogy is assumed).In the simple gradient diffusion hypothesis (SGDH), turbulent diffusion of some scalar quantity 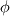 is modelled as: is modelled as: Here, 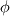 represents a concentration for turbulent mass transfer, or temperature for turbulent heat transfer. The eddy diffusivity can also be written in terms of the turbulent Schmidt number (for turbulent mass transfer), or the turbulent Prandtl number (for turbulent heat transfer). represents a concentration for turbulent mass transfer, or temperature for turbulent heat transfer. The eddy diffusivity can also be written in terms of the turbulent Schmidt number (for turbulent mass transfer), or the turbulent Prandtl number (for turbulent heat transfer).Now, in the transport equation for the TKE ( 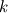 ), the diffusion term is modelled using SGDH: ), the diffusion term is modelled using SGDH: Questions 1. Does the eddy diffusivity for mass/momentum/heat transfer also depend on the quantity being transported like it does in molecular diffusivity? I would assume that it's a flow property, but I've read some articles saying that it's also dependent upon the molecular Prandtl and Schmidt numbers, which leads me to believe it's also a fluid property. If this is so, why are the Prandtl and Schmidt numbers universally set to 0.7 or unity regardless of the quantity being transported? 2. If the scalar being transported is not temperature, then does the SGDH assume turbulent diffusion occurs in the form of turbulent mass transport? If so, when would turbulent momentum transport come into play? To be honest, I don't fully understand the distinction between the two turbulent processes. 3. In the above equation where the diffusion term in the TKE equation is modelled using gradient diffusion, some sources say  is the turbulent Prandtl number, and some say it's the turbulent Schmidt number. Why is there this discrepancy? Both numbers are, in general, different (unless one assumes all the eddy diffusivities to be equal as per the Reynolds analogy). I would assume that is the turbulent Prandtl number, and some say it's the turbulent Schmidt number. Why is there this discrepancy? Both numbers are, in general, different (unless one assumes all the eddy diffusivities to be equal as per the Reynolds analogy). I would assume that  should be the turbulent Schmidt number as temperature is not the scalar being transported. I've also seen should be the turbulent Schmidt number as temperature is not the scalar being transported. I've also seen  being referred to as the "turbulent Prandtl-Schmidt number for being referred to as the "turbulent Prandtl-Schmidt number for 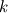 ", and I'm not sure what that refers to. I'm assuming it's probably saying it can be either the turbulent Prandtl or the turbulent Schmidt numbers, which doesn't make sense to me as discussed. In addition, the fact that it said "for ", and I'm not sure what that refers to. I'm assuming it's probably saying it can be either the turbulent Prandtl or the turbulent Schmidt numbers, which doesn't make sense to me as discussed. In addition, the fact that it said "for 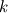 " also leads me to believe that the diffusivity depends on the scalar being transported as stated in my first question. In Popes book, he also defines individual Prandtl numbers for TKE and the dissipation rate, so it sounds like it depends on the quantity being transported? Again, I'm not sure why he's using a turbulent Prandtl number rather than a turbulent Schmidt number since it's not temperature being transported. " also leads me to believe that the diffusivity depends on the scalar being transported as stated in my first question. In Popes book, he also defines individual Prandtl numbers for TKE and the dissipation rate, so it sounds like it depends on the quantity being transported? Again, I'm not sure why he's using a turbulent Prandtl number rather than a turbulent Schmidt number since it's not temperature being transported.Any help would be much appreciated! Feel free to explain it like I'm 5 as I don't really have a good grasp of these concepts. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
1. The turbulent diffusivities are indeed flow properties. The molecular Prandtl number is often set to 0.7 or 1 depending on the fluid being modeled. Same with Schmidt number. They are not universally set. The turbulent Prandtl number is sometimes "universally" set to 0.8 due to a blatant lack of a turbulent heat flux model. Likewise, turbulent Schmidt numbers often get set to 1 due to a lack of any turbulent transport model. In short, the Reynolds analogy is being blatantly assumed. They are not universal, there just isn't any good model for them yet.
2. Turbulent momentum transport is the Reynolds stress in the momentum equation. For other quantities, turbulent velocity fluctuations are responsible for the turbulent fluxes of those respective quantities. That is, u', v', and w' are explicitly involved. You have misunderstood the gradient diffusion hypothesis, or maybe you are just calling terms by the wrong name. The GDH does not model turbulent diffusion, the GDH models turbulent transport as diffusion. Quote:
3. You are right that each number is different. It just depends who you ask. Prandtl number is generally reserved for the heat equation. But some people will call other turbulent eddy numbers turbulent Prandtl numbers (Fluent does this for example). Other people will call all of them turbulent Schmidt numbers (Star-CCM does this for example). It's a turbulent something number. Since all of them are attempting to mimic a molecular diffusion-like process, turbulent Schmidt number (being related to molecular diffusivity) makes more sense (to some people) to refer to the turbulent-number-thingy for other transport equations. There isn't universal agreement on what to name these things for variables like k. There isn't enough history to name them after famous people like Prandtl or Schmidt. Maybe if you wait another 100 years or so, the turbulence community will name it after somebody. For whatever reason, people don't like to call it the turbulent eddy diffusivity for k but rather call it the turbulent-Schmidt/Prandtl number for k (which isn't any less of a mouthful). At the same time... most ppl will call it turbulent viscosity (but not turbulent eddy viscosity for momentum). It's just personal preference. But since the Reynolds transport theorem is the same for all transported quantities, it's common in documentation to find the turbulent-numbers called the same turbulent Prandtl/Schmidt number for xxxxx with the understanding that each one should be the number for that particular transport quantity. But you are correct that they are in general all different, distinct, turbulent eddy numbers that are completely unrelated to one another. |
||
|
|

|
||
|
|
|
#3 |
|
Member
BM
Join Date: Sep 2021
Posts: 35
Rep Power: 5  |
Thank you, your response gives a lot of clarity and much needed context. I'll have to mull it over a bit more to process everything.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Even if largely adopted, the eddy diffusivity model for thermal problems is debated since 1962:
Lilly, “On the numerical simulation of buoyant convection,” Tellus 15, 148 (1962). |
|
|
|

|
|
|
|
|
#5 | |
|
Member
BM
Join Date: Sep 2021
Posts: 35
Rep Power: 5  |
Quote:
|
||
|
|

|
||
 |
| Tags |
| eddy diffusivity, gradient diffusion, prandtl, schmidt, turbulent diffusion |
|
|