 |
|
|
[Sponsors] | |||||
On the Roe approximate Riemann solver in the preconditioned density based method |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
I don't know if this will help you:
Initially consider only the conservative Jacobian without preconditioner with ![\boldsymbol{Q}=
\begin{pmatrix}
\rho \\[0.2em]
\rho u \\[0.2em]
\rho e
\end{pmatrix}=
\begin{pmatrix}
\alpha \\[0.2em]
\beta \\[0.2em]
\gamma
\end{pmatrix},
\quad \boldsymbol{F}(\boldsymbol{Q})=
\begin{pmatrix}
\rho u \\[0.2em]
\rho u^2 + p \\[0.2em]
u \left( E + p \right)
\end{pmatrix}=
\begin{pmatrix}
\beta \\[0.2em]
\beta^2/\alpha + p \\[0.2em]
\beta \gamma/\alpha + p \beta/\alpha
\end{pmatrix}, \boldsymbol{Q}=
\begin{pmatrix}
\rho \\[0.2em]
\rho u \\[0.2em]
\rho e
\end{pmatrix}=
\begin{pmatrix}
\alpha \\[0.2em]
\beta \\[0.2em]
\gamma
\end{pmatrix},
\quad \boldsymbol{F}(\boldsymbol{Q})=
\begin{pmatrix}
\rho u \\[0.2em]
\rho u^2 + p \\[0.2em]
u \left( E + p \right)
\end{pmatrix}=
\begin{pmatrix}
\beta \\[0.2em]
\beta^2/\alpha + p \\[0.2em]
\beta \gamma/\alpha + p \beta/\alpha
\end{pmatrix},](/Forums/vbLatex/img/fc7ed93e20efb23069c97fbd50274aa8-1.gif) and the pressure  defined as a function of all conservative variables. defined as a function of all conservative variables.For non-ideal gases the crucial part is derive consistent Roe partial derivatives to fulfill following relation  One approach may be the Liou-Glaister generalization. Here you initially calculate the partial derivatives point-wise with the EOS with the classical Roe averages (denoted with a tilde symbol). They do not fulfill the first relation and result in a wrong 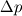 (origin of instability). (origin of instability).  After that you correct them by a projection method (denoted with a hat symbol)  where    with  Now in analogy to that you may approach in a similar way for the preconditioner version by considering the two equations  and  to derive consistent primitive partial derivatives. The approach is well described in the paper of Mottura. Regards
__________________
Check out my side project: A multiphysics discontinuous Galerkin framework: Youtube, Gitlab. Last edited by Eifoehn4; March 15, 2022 at 14:59. |
|
|
|

|
|
|
|
|
#22 |
|
Senior Member
|
Quote:
 at numerator over D is necessarily not 0, to a case where, instead, it should be (but isn't, maybe only because I don't know how to write it with my variables). However, I might still use the idea to actually check what I'm doing. at numerator over D is necessarily not 0, to a case where, instead, it should be (but isn't, maybe only because I don't know how to write it with my variables). However, I might still use the idea to actually check what I'm doing.For now, my euristic explanation for the matter is that, looking at my final dissipation vector here, my d1 component, which appears on all the equations, starts with drho/dT and all the other terms have rho_ROE inside, so drho/dT should sort of have it as well. |
|
|
|

|
|
|
|
|
#23 |
|
Senior Member
|
Quote:
 and and  . So, in the end, the heuristic reasoning on . So, in the end, the heuristic reasoning on 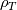 still looks legit. still looks legit.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure based and Density based Solver | Xobile | Main CFD Forum | 39 | August 19, 2020 07:04 |
| Approximate Riemann solver and reconstruction | TurbJet | Main CFD Forum | 2 | June 14, 2020 10:02 |
| Density and Pressure based solver | Diger | ANSYS | 1 | May 2, 2018 00:51 |
| Density or Pressure based solver | Achu | FLUENT | 1 | April 27, 2018 05:34 |
| Pressure based and Density based Solver | taekyu8 | FLUENT | 0 | January 28, 2013 12:05 |