 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Hi all,
I am looking at this Energy spectrum in the wavenumber domain. The dashed line is the Nyquist wavenumber. My question is: how is it possible that results are shown after the Nyquist wavenumber? Shouldn't that be the limit after that there are no value? |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
Right, the extension of the spectra from a numerical simulation cannot be extended for k>Kc. You should check for more details, is that from a published paper? |
||
|
|

|
||
|
|
|
#3 |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Thanks for your answer. It is the verification guide of FDS that you can find here https://pages.nist.gov/fds-smv/manuals.html. There is a chapter about turbulence from page 45 to 53. I cannot understand how can they have value after kc. Maybe they apply Taylor hypothesis?
|
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
From what I understand, the numerical simulation has greater resolution (64^3) than the CBS (32^3) and they adopted an explicit filter. Therefore, the extension of the spectra is reported until the numerical Nyquist frequency of the finer grid. |
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
The filter in FDS is implicit, as attached. The CBS is the experiment of Comte Bellot and Corrsin, the two top figure are related to the 32^3 the bottom two 62^3. I really cannot understand
|
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
Actually, what I really do not understand from the figures is the number of wavenumber components reported. In the top figure, the grid is 32^3, that is the spectra should be reported for 16 wavenumbers. On the bottom (64^3), the number of components should be 32. But if you count the circle you see that they are doubled, creating a fictious doubled Nyquist frequency.My opinion is that either they wrongly performed the FFT or the number of grid in each direction has to be doubled. You should ask to the author of the verification. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Ok. Thank you
 I will do that. I wanted simply to be sure that my doubts are lecit. I have also an other question about the subgrid model, but I will open an other thread I will do that. I wanted simply to be sure that my doubts are lecit. I have also an other question about the subgrid model, but I will open an other thread
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
From the figure, the Nyquist line seems at different wavenumbers. For example, in the 32^3 grid it appears exactly at the wavenumber 16 |
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#11 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
If the spectra is along r you should consider a sphere in the box, if the radius is greater than L you have spurious wavenumbers. However, the figures in the FDS file have no clear explanation. |
||
|
|

|
||
|
|
|
#12 | |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Quote:
I didn't understand a thing. Also if we make a 3D spectrum, how is it possible to see the wavenumberS after the nyquist wavenumber? shouldn't it be the limit? Does this change in a 3D contest? |
||
|
|

|
||
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
In isotropic homogeneous turbulence, the statistics are the same under rotation and traslation, this way the spectrum E11,E22,E33 has the same behavior. And the spectrum computed for a sphere of radius r=L should be also the same.
If you want to assume that dr=sqrt(dx^2+dy^2+dz^2) then you have the Nyquist frequency pi/dr but this is not what I see in the figure |
|
|
|

|
|
|
|
|
#14 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#15 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
||
|
|

|
|
|
|
|
#16 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
I only wanted to show, what the authors may have done numerically. Perhaps the explanation is not quite well.
|
|
|
|

|
|
|
|
|
#17 | |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Quote:
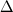 ,which they use as Filter, the geometric mean ,which they use as Filter, the geometric mean ![\sqrt[3]{\Delta x\cdot\Delta y\cdot\Delta z} \sqrt[3]{\Delta x\cdot\Delta y\cdot\Delta z}](/Forums/vbLatex/img/e21e1168c8d97452f0ed5099054d147d-1.gif) . . Actually this leads to a discrepancy in the 3d spectra the Nyquist wavenumber is not the filter limit. Could be? |
||
|
|

|
||
|
|
|
#18 | |
|
New Member
Join Date: Feb 2021
Posts: 13
Rep Power: 5  |
Quote:
Is this the theoretical Nyquist number with 2 points, or is it the numerical one for the discretization scheme? Not familiar with FDS, but if it uses an an implicit filter plus finite volume scheme, then the spectrum can contain infinite frequencies. The cut off wavenumber reported can thus be the theoretical or numerical, but depending on how the FFT is done on the finite volume solution, there can be very high frequencies present. The spectra shown here are nothing unusual for an implicit filter. |
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
The Nyquist frequency is identified by the grid size, no matter about which numerical method is used. The filter width identifies the Nyquist frequency only for spectral methods, otherwise pi/Delta is not equal to pi/h.
|
|
|
|

|
|
|
|
|
#20 |
|
New Member
Join Date: Feb 2021
Posts: 13
Rep Power: 5  |
I agree. But the question is different: is the line in the plot: Nyquist number (theoretical) or cut off number of the FDS scheme? Also, second question, how is the finite volume solution interpolated to do FFT?
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Length Scale - Wavenumber Context | Falu | Main CFD Forum | 3 | April 26, 2021 08:10 |
| Difference between Kolmogorov wavenumber and FFT wavenumber? | Falu | Main CFD Forum | 3 | January 12, 2021 12:31 |
| Wavenumber in L.E.S. | derz | CFX | 3 | July 27, 2015 09:05 |
| The wavenumber in the jet flow | jollage | Main CFD Forum | 1 | March 28, 2015 06:29 |
| Wavenumber | anuroopak | Tecplot | 0 | September 15, 2014 08:41 |