 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
|
|
|
#22 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,764
Rep Power: 66    |
The typical definition of autocorrelation is indeed:
 For infinite duration signals, you just take the limit as the signal length goes to infinity. I'm going to replace T with the signal length L because I like to use T for the period T. If the function is periodic over length T, then any integral of length T is the same for any t. 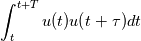 If my signal is length L, its autocorrelation function is (writing the same formula as before but with L instead). 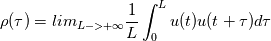 All I do is expand the summation using algebra. 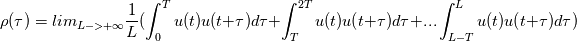 All those integrals being the same... I can replace them all with integrals from 0 to T. The signal length being L, I will have L/T such integrals. 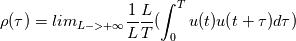 The L's cancel and the limit becomes trivial 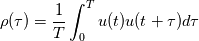 And we are back at the original definition of autocorrelation for a finite length signal. This is the periodic extension property I first mentioned. When you take the auto-correlation of a finite length signal, it's equivalent to taking the autocorrelation of the periodic extension of that signal. This is why aliasing occurs if you sample a signal different from its periodicity. Also why zero padding works (and is a very good idea in certain situations), etc etc. After writing this I realized the periodicity is not so obvious nor relevant for turbulent flows. It might be better to stick to the original definition involving 1/T for pedagogical purposes. But these properties are at play when you take Fourier transforms. I emphasize again that even if your signal is finite and not periodic, if you take the auto-correlation, you are looking at the autocorrelation of its hypothetical periodic extension. So where did the 1/T go? The one missing the 1/T is for finite waveforms!  What we mean by finite waveform is we observe a single impulse like event. For example, nothing, a single-square wave, and then nothing as opposed to a repetition of square waves. So if your data is [1,2,3] and you use the autocorrelation formula with 1/T, you are assuming that the data would have repeated itself [1,2,3,1,2,3,1,2,3,...]. Question is whether or not your data would-have repeated itself. That's how you choose which approach. |
|
|
|

|
|
|
|
|
#23 |
|
Senior Member
luca mirtanini
Join Date: Apr 2018
Posts: 165
Rep Power: 8  |
Thank you very much @LuckyTran ! This clarifies everything!
|
|
|
|

|
|
|
|
|
#24 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Of course, to make sense without the term 1/T the function must be integrable. However, the dimension of rho(tau) (if not specified differently) is different.
Moreover, consider that we are talking about a convolution product, it is easy to see the Fourier transform as the product of the transformed kernel. |
|
|
|

|
|
 |
| Tags |
| autocorrelation, power spectrum |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Power Spectral Density - Energy Spectrum | lucamirtanini | Main CFD Forum | 34 | April 8, 2022 20:40 |
| Power spectrum. | Jake. | Main CFD Forum | 1 | October 9, 2004 16:18 |