 |
|
|
[Sponsors] | |||||
|
|
|
#21 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
So now you have the initial value problem.
If the initial value is 0. The change when the initial value is 0 is 0. Hence, when it is 0, it stays 0. There are numerous analogues. The simple harmonic oscillator for example is y''=y. If you put y(t=0)=0, then y''=y'=y=0. A simple harmonic oscillator doesn't oscillate if there is no initial oscillation even though the system is capable of oscillating. |
|
|
|

|
|
|
|
|
#22 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Ok, let use the equation and integrate exactly in time z(t)=z(t0) + Int[t0,t] z(tau).Grad v(tau) dtau note that we integrate along the path-line dx/dt=v[x(t),t]. Thus, z(t) is a non-vanishing function if along the path-line there is a non-zero contribution of the integral. |
|
|
|

|
|
|
|
|
#23 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
But for the case of vorticity that you need only one initial vvalue I agree |
||
|
|

|
||
|
|
|
#24 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
So now it is suddenly obvious how y(t=0)=0 does not necessarily imply y'(t=0)=0?
Interesting..... So do you get it now? |
|
|
|

|
|
|
|
|
#25 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
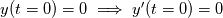 . I said that . I said that 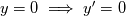 . These things are different. . These things are different. 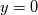 is the same thing as is the same thing as 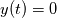 that implies that implies 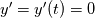 . Just like . Just like 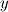 , which is not an independent variable here but a function of time ( , which is not an independent variable here but a function of time (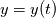 ), vorticity ), vorticity 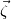 is a function of time and space ( is a function of time and space (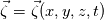 ), and not an independent variable. So setting ), and not an independent variable. So setting 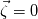 , is like saying that , is like saying that 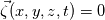 which definately implies that which definately implies that 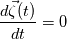 . One the other hand setting . One the other hand setting 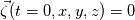 does not implies that does not implies that 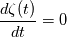 , or , or 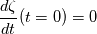 (assuming of course that you don't know the pde) (assuming of course that you don't know the pde)The point is that now I understand what you say, about knowing the initial value 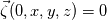 , and then calculating from the equation of vorticity the time derivative at t=0 , and then calculating from the equation of vorticity the time derivative at t=0  can lead as to the colclusion that can lead as to the colclusion that 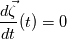 I just think, the way I would explain it now is this: we have this pde  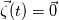 is a solution to this pde, because it satisfies the equation. is a solution to this pde, because it satisfies the equation. 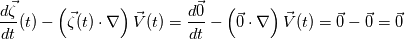 THOUGH, It doesn't satisfies EVERY initial condition. In case that the initial condition is  , then this solution satisfies both the pde and the initial condition. , then this solution satisfies both the pde and the initial condition.So we can say 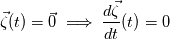
|
||
|
|

|
||
|
|
|
#26 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
That point is that you don't know y'(t=0) is anything until you apply it to the PDE regardless of what y(t=0). You are saying it... I really don't get why you don't understand your own words and why you're confusing yourself.
Note that these two statements are not equivalent: 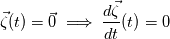 is trivial because as you write is trivial because as you write  . It's trivial because this is true , everywhere, all the time and has nothing to do with PDE's. The derivative of a constant function is 0. . It's trivial because this is true , everywhere, all the time and has nothing to do with PDE's. The derivative of a constant function is 0.What you want to write is: 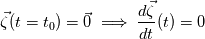 for any/all real t. This statement is only true due to the vorticity transport equation for this particular case of inviscid irrotational flow and under the condition that the vorticity was zero at least once. for any/all real t. This statement is only true due to the vorticity transport equation for this particular case of inviscid irrotational flow and under the condition that the vorticity was zero at least once.I know I didn't fully write out in detailed explicit notation what was meant by my words, but you cannot fancy it up and improperly insert notation because you can end up writing something inconsistent. |
|
|
|

|
|
|
|
|
#27 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Why? The derivative is still a function of time, you cannot assess in general this conclusion. |
|
|
|

|
|
|
|
|
#28 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
||
|
|

|
|
|
|
|
#29 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I don't agree with the part highlighted in red. You can easily see that z(t)=z(t0)+(t-t0)*dz/dt|t0 + (t-t0)^2/2 *d^2z/dt^2|t0 + ... Therefore you have to assess that all derivatives are zero, not only the first derivative. In your case, dz/dt|t0=0 does not imply that dz/dt(t) is zero for all time. |
|
|
|

|
|
|
|
|
#30 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
In the red highlighted part l didn't mean tha l came to this conclusion without the part bellow. |
||
|
|

|
||
|
|
|
#31 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
You wrote:
Quote:
I wrote the Taylor expansion in time that shows you can have a non-vanishing functions z(t) and z'(t) even if z(t0)=0 and z'(t0)=0. |
|
|
|

|
|
|
|
|
#32 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
The key is that you want to start assuming z(t)=0. Actually, we have only the equation and the initial condition at t0, no more conditions are assumed.
|
|
|
|

|
|
|
|
|
#33 |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
I know saying 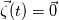 is a trivial solution. But if it satisfy my initial condition, it is the solution is a trivial solution. But if it satisfy my initial condition, it is the solution
|
|
|
|

|
|
|
|
|
#34 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
I said z(t)=0 is a solution, because it satisfies the equation. If z(t)=0 satisfies the initial condition too, it is the solution |
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No, the mathematical problem is: PDE+intial conditions+boundary conditions. You cannot get a solution only if you satisfy the intial conditions. The vorticity equation for ideal fluid is hyperbolic and requires BCs on an open space-time domain. Your trivial solution must satisfy also the BC on the frontiers. |
||
|
|

|
||
|
|
|
#36 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
|
||
|
|

|
||
|
|
|
#37 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Of course, if you set a zero initial condition and zero BC on the frontier.
|
|
|
|

|
|
|
|
|
#38 | |
|
New Member
Join Date: Jul 2022
Posts: 20
Rep Power: 4  |
Quote:
Thinking of a body starting to move at t=0, then z is everywhere zero at t=0 and after that is zero far away from the body at all directions for t>0. |
||
|
|

|
||
|
|
|
#39 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
You are in the field of the classic aerodynamics, now. Since you have slip condition on a body, the vorticity on a wall is not regular. You have to think to inviscid flow problems that are solved also with vorticity distribution. Lift is generated this way. |
||
|
|

|
||
|
|
|
#40 | |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Quote:
The thing is...this is not a proof. You are assuming the conclusion as a premise which is circular reasoning. It is a common mistake in inductive arguments so don't feel too bad about it. Btw the proof is not actually complicated nor profound. Filippo has basically demonstrated it for you, it falls right out after you apply the fundamental theorem of calculus. The crux is that you need to prove that the lagrangian derivative is zero for all time. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| interFoam inviscid and rotational | pablodecastillo | OpenFOAM Running, Solving & CFD | 7 | June 16, 2012 09:15 |
| Convergence for inviscid flow over sylinder | Rjakk | Main CFD Forum | 2 | March 21, 2007 11:53 |
| Inviscid flow | Atit Koonsrisuk | CFX | 12 | January 2, 2003 13:40 |
| Separation by Euler equations | Jitendra | Main CFD Forum | 9 | July 5, 2000 15:58 |