 |
|
|
[Sponsors] | |||||
[LES] Subgrid-scale and grid-scale energy equations |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Hello,
I'm reading some books about LES, in most of them, there are two equations about grid-scale and subgrid-scale energy equations. But none of them explain that how did they achieve these equations. And they also didn't refer to a source! For example: Can someone please explain to me that how these relations obtained? Or at least give me a reference? Best regards |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
|
If you know how to obtain the total kinetic energy equation (by multiplying each momentum equation for the respective velocity component and summing them), you can do the same for the resolved kinetic energy equation (using the resolved velocity and momentum equations). Then the sgs kinetic energy equation is obtained by difference between the two
|
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
But as you can see in rhs of first equation there is filtered(p*u) [second term in parenthesis] I don't think that it can be obtained without modeling (just like filtered(uv))! Then why is it there in the resolved part equations? |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
Here it is: https://www.springer.com/gp/book/9783319453026 |
||
|
|

|
||
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
It is clearly an error in the equation |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Hello,
Thanks for your reply. Yes. That seems to be an error because in this article that problem does not exist. U. Piomelli and J.R. Chasnov. Large-eddy simulations: Theory and applications. 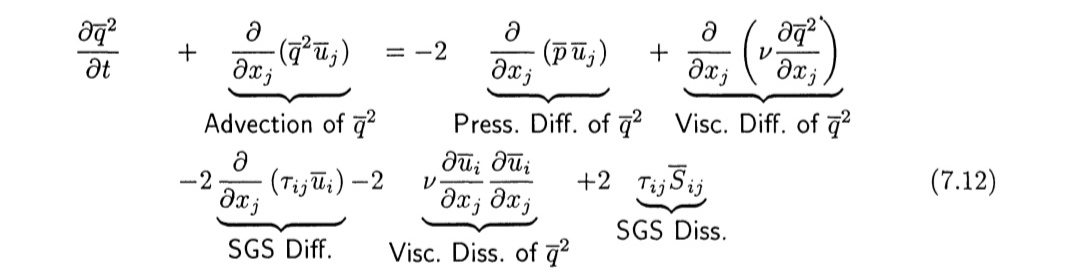
|
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Hello,
I just found something confusing about these equations. The derived equations are based on: 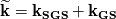 GS: Grid-Scale | SGS: SubGrid-Scale Where 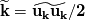 and and 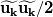 Please note that 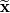 means filtered value of means filtered value of  . .The author emphasizes: "It is often misinterpreted that the sum of the grid-scale and subgrid-scale energy 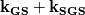 is is  . However it should be noted that this sum should be . However it should be noted that this sum should be 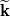 . The kinetic energy distribution from experiments or DNS should be filtered when LES results are compared with such results." . The kinetic energy distribution from experiments or DNS should be filtered when LES results are compared with such results."This means that 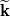 is the filtered DNS or experimental kinetic energy instead of the total kinetic energy. Then why it's not like the following equations just the same as filtered N-S equations? is the filtered DNS or experimental kinetic energy instead of the total kinetic energy. Then why it's not like the following equations just the same as filtered N-S equations?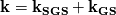 and and 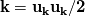 Why should the kinetic energy of DNS or experimental data be filtered when comparing with LES? If we filter DNS, then we only have the scales which have the size of the grid cell. While the LES data contains these scales + modeled small scales! |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
Ok, my last sentence in the post above [LES] Subgrid-scale and grid-scale energy equations was actually misleading as few details were missing.
Let me recap differently: 1) Kinetic energy of all the scales is 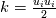 . Its equation is derived from taking the scalar product . Its equation is derived from taking the scalar product 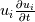 . Also . Also 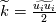 2) The kinetic energy of the grid scales is 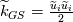 . Its equation is derived from taking the scalar product . Its equation is derived from taking the scalar product 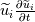 3) The filtered kinetic energy of the subgrid scales is 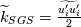 . Its equation is derived from the filtered scalar product . Its equation is derived from the filtered scalar product 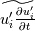 . Where . Where 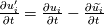 (and, obviously, (and, obviously, 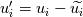 ) )4) The whole SGS stress tensor with the so called Leonard triple decomposition is 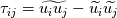 . Note that . Note that 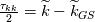 is known in LES as the Generalized SGS kinetic energy is known in LES as the Generalized SGS kinetic energy 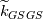 5) The unsolved kinetic energy is 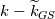 Now: - The kinetic energy of the book you are referring to is the one in 4 (i.e., 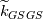 ) )- The common SGS kinetic energy usually referred to in LES is the one in 3 (see, for example, Sagaut) - The one I was referring to in my post is the one in 5 Which one you should refer to is really just a matter of definitions. But, obviously, they have different properties. |
|
|
|

|
|
|
|
|
#10 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
Why did you say that kinetic energy of all scales is also 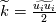 ? (Last equation of part 1) ? (Last equation of part 1)I think it shouldn't be filtered. Because if it is filtered,then we will not have small scales. |
||
|
|

|
||
|
|
|
#11 | ||
|
Senior Member
|
Quote:
Why the Sagaut reference has such definition has, of course, the same reason behind it. Because other people used it with that definition. Now, if you want me to further dig into this and explain why these people used this specific definition, it is a little more complex. The general answer is because that is the quantity that they ended up with in their equations. The unfiltered counterpart of that quantity is of relatively scarce interest because it is a quantity you don't know on scales you don't have access to. The filtered counterpart instead is used by several authors as base equation for 1 equation SGS LES models (in this case it is fundamental that it refers to scales you have access to, i.e., that it is filtered). Quote:
1) The conventional definition for the kinetic energy of all the scales is 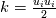 . Its equation is derived from taking the scalar product . Its equation is derived from taking the scalar product 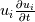 . .2) From 1, filtering both sides of the k defintion, obviously follows that 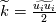
|
|||
|
|

|
|||
|
|
|
#12 |
|
Senior Member
|
My personal experience with several CFD books (altough not this one in particular, as I haven't read it) is that turbulence modeling, and LES in particular, is not something that can be trusted on that sources. They basically have to treat it but, trust me, there is no single general CFD book that treats it correctly.
In LES this is worst because even the two books of Sagaut (there is also a compressible version) are not enough to completely describe all the known approaches, and in some spots it has to treat some stuff by blindly reporting only some specific point of view. Now, if you just want a general grasp of the matter, just play along. But if you want to get into the equations, my suggestion is to first read Turbulent flows by Pope (in all its parts) and then go with Sagaut. |
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
I appreciate your help. You are right, but Sagaut's book is a hard-to-read book. I thinks it's really hard for a beginner. And I think this time, found an error in Sagaut's book:  In the term XII, i should be replaced by j because it leads to continuity equation and becomes zero. By the way. Thanks for your patience and great replies. |
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
|
Maybe you mean some other term (but there were no errors last time I did it myself), but XII is certainly correct. It is the diffusion term and there is no continuity involved... moreover, as this is a scalar equation, each term is scalar, so any index must be a repeated one (it must appear twice, meaning summation over that index), and while it is ugly to change the repeated index between different terms, it is actually fully customary which one you pick, might even be a or any other symbol
|
|
|
|

|
|
|
|
|
#15 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
I was reading two books with different inde and symbols at the same time and got confused! Thanks a lot |
||
|
|

|
||
|
|
|
#16 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
How did you notice that XII term is diffusion? Why didn't you say it's about dissipation? Why do we sort XII as diffusion, but X as dissipation? The same question stands for IX which is labeled as a dissipative term and XIII which labeled as a production term. Does it come from the mathematical for of the terms or it's just due to the physical understanding of the terms? Best Regards |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The dissipation of kinetic energy is a well defined term, it is mu*D  . It is characterized to be alway positive . It is characterized to be alway positive
|
||
|
|

|
||
|
|
|
#18 | |
|
Senior Member
Join Date: Jan 2018
Posts: 121
Rep Power: 8  |
Quote:
Apart from definitions, I just wanted to know is there any mathematical technique to sort the terms by their dissipative or diffusive nature? |
||
|
|

|
||
|
|
|
#19 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The meaning of a "diffusive term" is much more general than the use done in the KE expressione. You should turn back to the origin of the term as defined in Chap 1 of Kundu |
||
|
|

|
||
|
|
|
#20 | |
|
Senior Member
|
Quote:
Don't take me wrong but, maybe, you should step back from LES in order to first clarify some basic concepts. The major risk here is investing time without a proper return. Also, as LES involves both numerics, fluid dynamics and turbulence, a strong background in all of them is required in order to understand it. Maybe you can still grasp some general concept, but then I see no point in trying to decode, say, the SGS kinetic energy equation. Just know that it is what it is and go over it. |
||
|
|

|
||
 |
| Tags |
| les, subgrid scale |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Different horizontal and vertical subgrid scale viscosities in LES | pablo | Fluent UDF and Scheme Programming | 0 | November 13, 2012 17:18 |
| Different horizontal and vertical subgrid scale viscosities in LES | pablo | FLUENT | 0 | November 13, 2012 16:26 |
| TUI command for grid scale in mm | Ralf Schmidt | Fluent UDF and Scheme Programming | 2 | March 16, 2009 07:06 |
| Reynolds transport, turbulence model, etc | Beginner | Main CFD Forum | 1 | January 7, 2009 06:36 |
| Combustion Convergence problems | Art Stretton | Phoenics | 5 | April 2, 2002 06:59 |