Finite Volume Simple Code Problem

DAVIDRASC · September 17, 2020, 04:55

Hi Everyone.I have wrote a FV SIMPLE code to solve fluid flow in a 2d rectangular channel. in straight channel every thing is OK! but the problem starts when I try to solve flow in a U-Type Geometry. Velocity has 2 component in X and Y direction (u,v). in my code results, u-component has a value throughout the domain but v-component is zero everywhere while its expected that in y-direction in channel, u-component be zero and v-component has value. Does any one know whats the problem?

https://www.cfd-online.com/Forums/at...1&d=1600329207

https://www.cfd-online.com/Forums/at...1&d=1600329677

The nodes arrangement is like below.

https://www.cfd-online.com/Forums/at...1&d=1600329300

sbaffini · September 17, 2020, 06:03

1) In general, I expect both components to actually have non zero values in this sort of duct, independently from the specific region. So I would check this first. Of course, the axial component is expected to be (much) larger than the transversal one (which, however, can't be zero)

2) From your node arrangement, it actually seems that your outcome is exactly what you have to expect, because along the y-aligned part of the channel you still have the i index varying along the axis, which is the same index varying along the axis of the x-aligned part of the channel. Still, I don't understand how you manage the indexing at the intersection

DAVIDRASC · September 17, 2020, 10:40

Quote:

Originally Posted by sbaffini

1) In general, I expect both components to actually have non zero values in this sort of duct, independently from the specific region. So I would check this first. Of course, the axial component is expected to be (much) larger than the transversal one (which, however, can't be zero)

2) From your node arrangement, it actually seems that your outcome is exactly what you have to expect, because along the y-aligned part of the channel you still have the i index varying along the axis, which is the same index varying along the axis of the x-aligned part of the channel. Still, I don't understand how you manage the indexing at the intersection

So thanks Paolo for your quick reply!
I wrote another code to generate this grid. The full geometry is as follow.

https://www.cfd-online.com/Forums/at...1&d=1600349460

Node indexing was regarded as body-fitted coordinate. I supposed after discretization of equations, we are faced with a set of scalar quantities that are independent of coordinate system. Am I wrong?
However, hat's the solution? what should I do? Thank you for guiding me

Eifoehn4 · September 17, 2020, 15:58

Please anser some necessary questions first:

What mathematical model do you use?
Is the problem transient or stationary?
What numerical methods do you use? Explizite? Implicite? What temporal discretization? What spatial discretization? First order? Seconde order? High Order?
What initial and boundary conditions do you use?
Since you are using non-Cartesian meshes do you consider any metric terms?

DAVIDRASC · September 18, 2020, 02:49

Quote:

Originally Posted by Eifoehn4

Please anser some necessary questions first:

What mathematical model do you use?
Is the problem transient or stationary?
What numerical methods do you use? Explizite? Implicite? What temporal discretization? What spatial discretization? First order? Seconde order? High Order?
What initial and boundary conditions do you use?
Since you are using non-Cartesian meshes do you consider any metric terms?

My equations are, Continuity and Momentum with some source terms.

https://www.cfd-online.com/Forums/at...1&d=1600407407

Problem in steady state in a 2d channel and numerical model is SIMPLE based on Finite Volume Method. spatial discretization is second order and I didn't use any metric terms.

Eifoehn4 · September 18, 2020, 05:51

This means you do not account for any deformed or stretched meshes?

You should consider that each cell might has a different area and that each side might has a different length with a different normal vector.

DAVIDRASC · September 18, 2020, 06:29

Quote:

Originally Posted by Eifoehn4

This means you do not account for any deformed or stretched meshes?

You should consider that each cell might has a different area and that each side might has a different length with a different normal vector.

Maybe I did not say exactly. Each cell was regarded as below

https://www.cfd-online.com/Forums/at...1&d=1600420627

Area of each cell was calculated by this equation:

https://www.cfd-online.com/Forums/at...1&d=1600420923

Moreover I replaced any DeltaX and DeltaY by DeltaKsi and DeltaEta:

https://www.cfd-online.com/Forums/at...1&d=1600421216

So each cell has its specific lenght, area and normal vector

sbaffini · September 18, 2020, 07:06

I am not an expert in structured, non cartesian, approaches requiring metric terms but, what is that you actually call u and v velocity components? Are they before or after any other metric transformation (which I expect to be necessary here to obtain the true cartesian components)? Could you be having an issue in the metric tranformations themselves?

Also, are we talking about exactly zero transverse velocity (yet, what we mean by transverse here has to be clarified in the context of your solver) or what?

DAVIDRASC · September 18, 2020, 09:38

Quote:

Originally Posted by sbaffini

I am not an expert in structured, non cartesian, approaches requiring metric terms but, what is that you actually call u and v velocity components? Are they before or after any other metric transformation (which I expect to be necessary here to obtain the true cartesian components)? Could you be having an issue in the metric tranformations themselves?

Also, are we talking about exactly zero transverse velocity (yet, what we mean by transverse here has to be clarified in the context of your solver) or what?

1. First I generated the geometry according to above mentioned indexing system.
2. Lengths, area and volume of each cell was calculated like this:

https://www.cfd-online.com/Forums/at...1&d=1600420627

3. Next, based on SIMPLE algorithm, Convection and Diffusion Term was calculated for each cell. DeltaX and DeltaY needed for these calculations were replaced by DeltaKsi and DeltaEta
4. Hybrid discretization scheme was selected to calculate coefficients (aW, aE, aN, aS).
5. Finally u, v (X-aligned and Y-aligned velocities) in accordance with inertial coordinate system is derived by prescribed steps defined by SIMPLE Method.

https://www.cfd-online.com/Forums/at...1&d=1600432548

6. It’s expected that u and v somewhat become like this.

https://www.cfd-online.com/Forums/at...1&d=1600432687
https://www.cfd-online.com/Forums/at...1&d=1600432713

But unfortunately results are something else!!!

Eifoehn4 · September 18, 2020, 12:19

Quote:

Originally Posted by DAVIDRASC

Maybe I did not say exactly. Each cell was regarded as below

https://www.cfd-online.com/Forums/at...1&d=1600420627

Area of each cell was calculated by this equation:

https://www.cfd-online.com/Forums/at...1&d=1600420923

Moreover I replaced any DeltaX and DeltaY by DeltaKsi and DeltaEta:

https://www.cfd-online.com/Forums/at...1&d=1600421216

So each cell has its specific lenght, area and normal vector

I dont know exactly what mathematical background your approach is based on. Anyway, consider an arbitrary field variable f as a function of $f(x(\xi,\eta),y(\xi,\eta))$ . Now you can start from the physical side

$\frac{ \partial f}{ \partial x} = \frac{ \partial f}{ \partial \xi} \frac{ \partial \xi}{ \partial x} + \frac{ \partial f}{ \partial \eta} \frac{ \partial \eta}{ \partial x},$
$\frac{ \partial f}{ \partial y} = \frac{ \partial f}{ \partial \xi} \frac{ \partial \xi}{ \partial y} + \frac{ \partial f}{ \partial \eta} \frac{ \partial \eta}{ \partial y},$

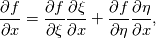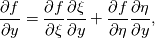resulting in

$\begin{pmatrix} f_x \\ f_y \end{pmatrix}= \begin{pmatrix} \xi_x & \eta_x \\ \xi_y & \eta_y \end{pmatrix} \begin{pmatrix} f_{\xi} \\ f_{\eta} \end{pmatrix}.$

Or you start from the other side with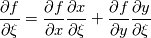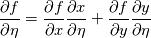

$\frac{ \partial f}{ \partial \xi} = \frac{ \partial f}{ \partial x} \frac{ \partial x}{ \partial \xi} + \frac{ \partial f}{ \partial y} \frac{ \partial y}{ \partial \xi}$
$\frac{ \partial f}{ \partial \eta} = \frac{ \partial f}{ \partial x} \frac{ \partial x}{ \partial \eta} + \frac{ \partial f}{ \partial y} \frac{ \partial y}{ \partial \eta}$

resulting in

$\begin{pmatrix} f_{\xi} \\ f_{\eta} \end{pmatrix}= \begin{pmatrix} x_{\xi} & y_{\xi} \\ x_{\eta} & y_{\eta} \end{pmatrix} \begin{pmatrix} f_{x} \\ f_{y} \end{pmatrix}.$

Now since both sides must be identical it holds

$\begin{pmatrix} \xi_x & \eta_x \\ \xi_y & \eta_y \end{pmatrix} = \begin{pmatrix} x_{\xi} & y_{\xi} \\ x_{\eta} & y_{\eta} \end{pmatrix}^{-1} .$

Before discretization you simply have to replace your derivative expressions with the relations above. Moreover after that you also have to discretize metric terms $x_{\xi}, y_{\xi}, x_{\eta}, y_{\eta}$ . Note for a simple low order FV method these are simply the normal or tangential vectors.

Regards

sbaffini · September 19, 2020, 05:37

Typically, as we can't get trough your code line by line, you would proceed by doing different tests from simple to complex until you spot what's wrong.

Now, you said that your straight channel works (and I assume we are talking about the exact same code running on a different case.

So, as next step, I suggest you to run the same straight channel but with a 45 degrees rotation of the grid. This should be much simpler to debug

FMDenaro · September 19, 2020, 06:46

Quote:

Originally Posted by sbaffini

Typically, as we can't get trough your code line by line, you would proceed by doing different tests from simple to complex until you spot what's wrong.

Now, you said that your straight channel works (and I assume we are talking about the exact same code running on a different case.

So, as next step, I suggest you to run the same straight channel but with a 45 degrees rotation of the grid. This should be much simpler to debug

I quote, but I would suggest to run the case of the backward facing step, try a laminar steady case, for example at Re=400.

sbaffini · September 19, 2020, 06:49

Considering your problem, actually, even a purely vertical straight channel is a test I would consider

DAVIDRASC · September 20, 2020, 15:21

Dear all! Many thanks for your valuable guidance. I think I found the problem to some extent according to your tips. In this case, although the generation of geometry is based on general coordinates, but the discretization of the equations, is carried out by the usual method.
For example in below equation, (pE-pW)*DeltaV/DeltaX is considered as [P(i+1,j)- P(i-1,j)] * DeltaV/[SQRT((Xp(i+1,j) - Xp(i,j))**2 + (Yp(i+1,j) - Yp(i,j))**2)] while The equations must be discretized in the manner indicated by Eifoehn4.

https://www.cfd-online.com/Forums/at...1&d=1600625974

In other word, all derivations in X (DeltaPHI/DeltaX) and Y (DeltaPHI/DeltaY) direction is written as [PHI(i+1,j) - PHI(i,j)] / [SQRT((Xp(i+1,j) - Xp(i,j))**2 + (Yp(i+1,j) - Yp(i,j))**2)]
and
[PHI(i,j+1) - PHI(i,j)] / [SQRT((Xp(i,j+1) - Xp(i,j))**2 + (Yp(i,j+1) - Yp(i,j))**2)] respectively.

SQRT((Xp(i+1,j) - Xp(i,j))**2 + (Yp(i+1,j) - Yp(i,j))**2) and SQRT((Xp(i,j+1) - Xp(i,j))**2 + (Yp(i,j+1) - Yp(i,j))**2) are distances between center point of 2 adjacent nodes.

Isn't that so?

September 17, 2020, 15:58		#4
Eifoehn4 Senior Member - Join Date: Jul 2012 Location: Germany Posts: 184 Rep Power: 14	Please anser some necessary questions first: What mathematical model do you use? Is the problem transient or stationary? What numerical methods do you use? Explizite? Implicite? What temporal discretization? What spatial discretization? First order? Seconde order? High Order? What initial and boundary conditions do you use? Since you are using non-Cartesian meshes do you consider any metric terms? __________________ Check out my side project: A multiphysics discontinuous Galerkin framework: Youtube, Gitlab.

September 18, 2020, 05:51		#6
Eifoehn4 Senior Member - Join Date: Jul 2012 Location: Germany Posts: 184 Rep Power: 14	This means you do not account for any deformed or stretched meshes? You should consider that each cell might has a different area and that each side might has a different length with a different normal vector. __________________ Check out my side project: A multiphysics discontinuous Galerkin framework: Youtube, Gitlab.

Similar Threads
Thread	Thread Starter	Forum	Replies	Last Post
how to set periodic boundary conditions	Ganesh	FLUENT	15	November 18, 2020 07:09
finite volume 2D matlab code	DJ4	CFD Freelancers	1	April 21, 2016 05:35
Finite volume NS equation solver code	Dansys	Main CFD Forum	1	November 17, 2014 12:19
Problem of simulating of small droplet with radius of 2mm	liguifan	OpenFOAM Running, Solving & CFD	5	June 3, 2014 03:53
doubt in finite volume code...	Dhileep	Main CFD Forum	1	January 29, 2009 08:31

September 17, 2020, 06:03		#2
sbaffini Senior Member Paolo Lampitella Join Date: Mar 2009 Location: Italy Posts: 2,192 Blog Entries: 29 Rep Power: 39	1) In general, I expect both components to actually have non zero values in this sort of duct, independently from the specific region. So I would check this first. Of course, the axial component is expected to be (much) larger than the transversal one (which, however, can't be zero) 2) From your node arrangement, it actually seems that your outcome is exactly what you have to expect, because along the y-aligned part of the channel you still have the i index varying along the axis, which is the same index varying along the axis of the x-aligned part of the channel. Still, I don't understand how you manage the indexing at the intersection

September 18, 2020, 07:06		#8
sbaffini Senior Member Paolo Lampitella Join Date: Mar 2009 Location: Italy Posts: 2,192 Blog Entries: 29 Rep Power: 39	I am not an expert in structured, non cartesian, approaches requiring metric terms but, what is that you actually call u and v velocity components? Are they before or after any other metric transformation (which I expect to be necessary here to obtain the true cartesian components)? Could you be having an issue in the metric tranformations themselves? Also, are we talking about exactly zero transverse velocity (yet, what we mean by transverse here has to be clarified in the context of your solver) or what?

September 19, 2020, 05:37		#11
sbaffini Senior Member Paolo Lampitella Join Date: Mar 2009 Location: Italy Posts: 2,192 Blog Entries: 29 Rep Power: 39	Typically, as we can't get trough your code line by line, you would proceed by doing different tests from simple to complex until you spot what's wrong. Now, you said that your straight channel works (and I assume we are talking about the exact same code running on a different case. So, as next step, I suggest you to run the same straight channel but with a 45 degrees rotation of the grid. This should be much simpler to debug

September 19, 2020, 06:49		#13
sbaffini Senior Member Paolo Lampitella Join Date: Mar 2009 Location: Italy Posts: 2,192 Blog Entries: 29 Rep Power: 39	Considering your problem, actually, even a purely vertical straight channel is a test I would consider