 |
|
|
[Sponsors] | |||||
Stability issues with "modified pressure-correction" scheme |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#41 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
I think you have not understood that. |
||
|
|

|
||
|
|
|
#42 | |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
Are you sure we're talking about the same FastPoissonSolver ? One like explained here ? http://citeseerx.ist.psu.edu/viewdoc...=rep1&type=pdf |
||
|
|

|
||
|
|
|
#43 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#44 | |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
possibly  as i said, i'm no expert on this. as i said, i'm no expert on this.i was only mentioning "FFT based FastPoisson solver" initially and the paper also talks about "solving directly using a fast Poisson solver". if you were interpreting this as something else then that would at least explain all this confusion. 
|
||
|
|

|
||
|
|
|
#45 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Ok, I read and indeed no pure spectral representation of the solution is implied, it is just a DST method to solve the second order accurate FD equation, like SOR or multigrid or GMRES method. I am not sure it is really computationally cheap... However, now we are sure that the method is congruent to the exact projection of Chorin and is second order in space. I suggest to test your code by starting with small density differences and then, if it works, increasing the density gap. Are you using a full explicit method for convection and diffusion? How do you set the time step for the numerical stability constraint? |
||
|
|

|
||
|
|
|
#46 | ||
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
Thanks god we sorted this out, haha  Actually it is very cheap compared to all alternatives. Especially on a GPU. My shader implementation needs 0.6ms on a 1024^2 grid (on a GeForce 1070). Quote:
I use the MacCormack scheme for advection. No explicit diffusion is added, neither are any forces. See my initial post. Even for very small time-steps/velocities of about 1/100 of a gridcell per timestep will make it blow up eventually. Also smaller density ratios will make it blow-up. It will just take a little longer. As stated, an exception is a density ratio of 1 in which case it works like a charm (but in that case the "modified" part of the pressure solver is not actually in effect). |
|||
|
|

|
|||
|
|
|
#47 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Well, actually you are solving Euler equations with an initial discontinuity. Without diffusion, using central space discretization, you will get strong oscillations and finally instability. Have a look to some shock capturing method based on the artificial dissipation method |
||
|
|

|
||
|
|
|
#48 | |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
What speaks against it is that NOT advecting the fluid will avoid the blow up and it stabilizes (with density ratio of 1000) to a nice solution of divergence free velocities (in which the water is mostly unaffected, and the air flows around it to counter divergence). here's a picture displaying vertical velocity color coded (green positive, red negative): https://ibb.co/GTCDZ81 (left initial condition, right solution after few iterations) |
||
|
|

|
||
|
|
|
#49 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#50 | ||
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
Thanks you for the references. Now it is more clear what you are doing. I would follow the hints made by FMDenaro. Moreover i think the key problem with high density ratios is this term in your modified equation: ![\dots = \nabla \cdot \left[ \left( 1 - \frac{ \rho_{0} }{ \rho^{n+1}} \right) \nabla \hat{p} \right] + \dots \dots = \nabla \cdot \left[ \left( 1 - \frac{ \rho_{0} }{ \rho^{n+1}} \right) \nabla \hat{p} \right] + \dots](/Forums/vbLatex/img/77fd17f946baf38f18194fab6327c27b-1.gif) How do you approximate this at the moment? Did you checked that this is correct? Edit: Quote:
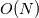 instead of instead of 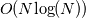 . .
|
|||
|
|

|
|||
|
|
|
#51 |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
you mean how do i approximate  ? as suggested in the paper as ? as suggested in the paper as 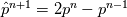 I tried with the Jacobi method at first but it fails miserably for high density ratios (meaning it converges extremely slowly). Also, just to be clear, I'm not looking for alternatives (as I have done so quite extensively), I'm trying to debug the issue with the paper in question  Debugging this remotely would deem extremely hard. That's why I was hoping with my initial post to find someone who has actually managed to implement the described algorithm successfully... |
|
|
|

|
|
|
|
|
#52 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
With two iterations it works quite well for constant density (just tested). But i think you are correct. When the density changes form 1 to 1000, the iterative Poisson solver has to do some work. |
||
|
|

|
||
|
|
|
#53 |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
The density gradient is not really needed, but the density at the position where the gradient is definied (between cells). This is done by linear interpolation (simple averaging) of the two neighboring cells as the paper suggests. |
|
|
|

|
|
|
|
|
#54 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
https://en.wikipedia.org/wiki/Rubber_duck_debugging In the meantime, maybe I or another guy in the forum will come up with another idea. |
||
|
|

|
||
|
|
|
#55 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
But what about your stability criterion? It seems your problem becomes stiff at high density ratio, I immagine you need some time step constraint to manage that. Furthermore, what about refining the grid? |
||
|
|

|
||
|
|
|
#56 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Have you also considered this discussion about the interface?
|
|
|
|

|
|
|
|
|
#57 |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
||
|
|

|
|
|
|
|
#58 | |
|
New Member
Join Date: Jun 2020
Posts: 27
Rep Power: 6  |
Quote:
It fluid gains momentum at the density transitions and making the timestep really small seems to just delay the problem. So it doesn't really serve as a solution, unfortunately. I suspect some tiny error in my code, yet i'm unable to find it 
|
||
|
|

|
||
|
|
|
#59 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
Yes, a bug in your code is possible, however reducing the time-step while using a first order upwind should be sufficient to get a stable solution. If that does not happen I would find about a bug for sure. |
||
|
|

|
||
 |
| Tags |
| modified solver, pressure based solver |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Pressure fields in FOAM, p field, total pressure, etc. | Tobi | OpenFOAM Post-Processing | 9 | March 25, 2022 02:33 |
| Wind tunnel Boundary Conditions in Fluent | metmet | FLUENT | 6 | October 30, 2019 13:23 |
| outlet pressure Boundary settings -velocity streamline under ambient temp.conditions | Vishnu_bharathi | CFX | 12 | November 21, 2017 07:56 |
| Setting up the pressure variation due to tornado in a duct(UDF)+animation | guillaume1990 | FLUENT | 0 | March 3, 2014 12:59 |
| Pressure BC for combustion chamber | Giuki | FLUENT | 1 | July 19, 2011 12:35 |