 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
|
Hi,
I've been reviewing the basic idea of FVM. However, there are few questions that I am confused. Lets take simple 1D linear advection for example 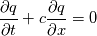
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
There is no conflict between the two textbooks. Leveque explains clearly the FV formulation in Eq.(4.1)-(4.6). You have to integrate over a finite volume and integrate further in time.
In the textbook of Ferziger you have to consider the section of the FVM starting from the integral form and you will see the same formulation. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
|
Roughly speaking, because LeVeque has to teach the whole thing also for non linear cases and for a very large family of equations. Ferziger mostly treats linear equations (with the mass flux already given), while the determination of the mass flux is made only with a specific implementation and equation in mind. Besides this, Ferziger uses the method of lines, while LeVeque mostly doesn't.
|
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
|
Quote:
Plus, is there any other higher order numerical flux? LeVeque extensively talks about Lax-Wendroff and Lax-Friedrichs, which only 2nd-order. |
||
|
|

|
||
|
|
|
#6 | |
|
Member
Join Date: Aug 2018
Posts: 77
Rep Power: 8  |
Quote:
yes, read up on ENO/WENO schemes. Chi Wang Shu comes to mind... |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
As a general rule the flux reconstrunction means:
- assuming that the averaged values Q are computed in each FV at time t0; - considering that the derivative in time dQ/dt depends on the difference of the fluxes on the faces, the fluxes depending however on q not on Q. - the reconstruction of the fluxes requires the time integration between t0 and t0+dt of the difference function F[q(Q)]i+1/2 -F[q(Q)]i-1/2. - high order accuracy means you have to implement both a high order time integration and a high order reconstruction q(Q) (like in ENO/WENO/TENO). Leveque provides many details for the one-dimensional equations (linear and non-linear) as well as for one-dimensional system of equations. Note that an example of high order reconstruction in 2d space is illustrated in the textbook of Ferziger but you can also see as further example the original QUICK/QUICKEST schemes of Leonard. |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
No, we don't have the face values for the flux as it would require the knowledge of the pointwise function q but we know the averaged function Q. Therefore, "reconstruction" is not a simple interpolation but the introduction of an approximation for the functional relation q=q(Q). |
||
|
|

|
||
|
|
|
#9 |
|
Super Moderator
|
If you reconstruct a unique value at each face (usually with a central stencil) then you use that to compute the flux. This would lead to central difference type schemes.
For convection dominated problems, say at high Re, you may want upwind schemes. You reconstruct two values at each face, one with a left biased stencil and another with right biased stencil. Then to compute the flux, you will need a numerical flux, which is the subject of LeVeque's book. |
|
|
|

|
|
|
|
|
#10 | ||
|
Senior Member
|
Quote:
Quote:
I went through Qiqi Wang's class at MIT (on YouTube). His explanation of reconstruction is (if I understand him correctly) "directly interpolate the flux", rather than interpolate the face value then compute the flux (as what I thought). How do you think about it? Last edited by TurbJet; January 30, 2020 at 15:42. |
|||
|
|

|
|||
|
|
|
#11 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Dear all,
i am a little bit confused nobody mentioned the Riemann problem theory (exact or approximativ), which is the most intuitive way to explain finite volume methods. Not only from a mathematical point of view but also from a physical one. If you succeed to understand what a Riemann problem is you won't have any problems to understand how finite volume methods work. Regards |
|
|
|

|
|
|
|
|
#12 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The Riemann problem at each face is one of the methods for the flux evaluation, starting from the hystorical Godunov method then developed by Roe.However, developing a high-order and multidimensional FVM based on Riemann solver is cumbersome. Furthermore, the typical field of application of Riemann solvers is for Euler equations where singularity (shock) appears. A different field is the Navier-Stokes equations at very low Mach (or incompressible assumption) where the flux reconstruction is based on different ideas and the pressure has not thermodynamics meaning. |
||
|
|

|
||
|
|
|
#13 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
Nevertheless, when the question arises about the motivation of the flux approximation in the context of finite volume methods then it is hard to give a vivid answer without this theory, especially if someone has not understand that the physical flux at the face boundaries is generally not unique with finite volume methods. Note that the Riemann problem theory does not only exist for compressible flows. For example the exact Riemann problem for a scalar transport equation is the upwind flux approximation. This will give you directly an answer why a central approximation is not recommended here. Beside the common compressible and incompressible Navier Stokes equations there exist other identical physical models which are purly hyperbolic (at least for the compressible one) and may completely be explained by the generalized Riemann theory, which does not neccessaraly be a constant initial value problem. Regards Last edited by Eifoehn4; January 31, 2020 at 03:52. |
||
|
|

|
||
|
|
|
#14 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Yes for a beginner or a more advanced CFD enthusiast i would recommend to not start with Ferziger book.
|
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
You are right if we consider only some specific aspects of the FVM that apply only to some cases, in particular to hyperbolic problems. For example the textbook of Leveque is well suited for such field. 1) central flux reconstruction is well suited for the incompressible form of the NSE, it is quite a standard in a lot of hystorical FV codes. The momentum equation is parabolic and the continuity is hyperbolic but is solved by trasforming in the elliptic equation. 2) The use of Riemann solver in a FVM is based on a discontinuity of values between the left and right faces but that says nothing about the way the averaged function behaves within each FV. It could be piece-wise constant or linear or quadratic and so on. This part is a key in the flux reconstruction out of the Riemann problem. As you wrote, we cannot express a unique primitive function from a known averaged value. 3) developing a high order accurate FVM base on the Riemann solver (more than the simple first order upwind in the Godunov method) is quite problematic in multidimensional flows. I think that is better to analyse differently FVM either for hyperbolic Euler equations or parabolic/elliptic NSE equations. Some standard CFD textbooks illustrates the FVM without considering at all the Riemann solver in the flux reconstruction. |
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
What book do you think is better for that? From my experience as teacher in the CFD field is quite problematic to introduce the FVM starting with the Riemann solver-based flux reconstrution. You need first a background in gasdynamics. |
||
|
|

|
||
|
|
|
#18 |
|
Member
Join Date: Aug 2018
Posts: 77
Rep Power: 8  |
Why would multi D Riemann solvers be important? all the FV codes I have seen in use at big conpanies just use 1D RP solvers normal to the faces...
|
|
|
|

|
|
|
|
|
#19 |
|
Senior Member
|
Yeah, I know the ENO family. But from what I read (Chi-Wang Shu, ENO and WENO for hyperbolic conservation law, ICASE, 1997), under FVM framework, ENO/WENO only reconstruct the left/right face values, which still need some numerical flux to approximate the physical one. And Shu recommended 3 numerical fluxes in this paper: 1. Gudonuv flux; 2. Enquist-Osher flux; 3. Lax-Friedriches flux.
From this paper, seems like only under FDM framework will ENO/WENO directly go ahead and reconstruct the fluxes. |
|
|
|

|
|
|
|
|
#20 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
In my opinion it is really helpful to introduced common finite volume approximations along with the Riemann problem theory. The books of Leveque and Toro are good references, but i would also suggest to use second literature, where the focus is more on numerical methods, especially for the incompressible Navier Stokes equations. Regards |
||
|
|

|
||
 |
| Tags |
| finite volume method, reconstruction scheme |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Computing the flux at an arbitrary 2D surface | andy_pr | OpenFOAM Programming & Development | 0 | August 7, 2018 15:23 |
| How to apply heat flux at the interface when using VOF method? | princekar | FLUENT | 0 | November 15, 2015 08:47 |
| Finite volume methods, reconstruction, etc. | Nereus | Main CFD Forum | 9 | January 31, 2012 17:12 |
| [Commercial meshers] ST_Malloc: out of memory.malloc_storage: unable to malloc Velocity SA, | cfdproject | OpenFOAM Meshing & Mesh Conversion | 0 | April 14, 2009 16:45 |