 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
AGN
Join Date: Dec 2011
Posts: 70
Rep Power: 14  |
Method of line (MOL) is a common way of solving a partial differential equation using numerical methods. Most of the software used for solving PDE is based on MOL. It can convert a PDE into ODE so numerical methods developed for ODE can be used. If MOL did not exist, it would be difficult to solve PDE. I want to discuss the one limitations of the method of line without using any approximate discretization scheme and want to know any existing alternatives for this.
The General form of advection equation is: 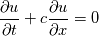 Using MOL, it reduced to ODE, that is: 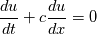 Let assume we an I.C 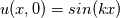 The analytical solution is: 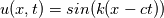 Assume that we are having a method that can exactly calculate the derivative and time integration. Then 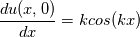 We shall try to solve this problem using the integral approach. Integrating and substituting derivative in MOL, it becomes 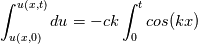 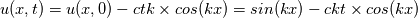 The difference between the solution obtained from MOL and the exact solution at first time step is: 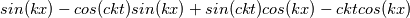 when 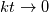 , this error become zero so the scheme is consistent. Because of consistency, it will lead to a relatively good solution but in some cases, it may not. , this error become zero so the scheme is consistent. Because of consistency, it will lead to a relatively good solution but in some cases, it may not. If 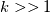 , we need very small , we need very small 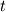 to make to make 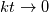 . The problem having high . The problem having high 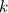 is high wave number problem. They are always difficult to solve using numerical methods. They always cause inherent stiffness in the solution. Usually, problems involving shocks have high wavenumber or inherent stiffness, so the error introduced by the numerical methods is relatively high. is high wave number problem. They are always difficult to solve using numerical methods. They always cause inherent stiffness in the solution. Usually, problems involving shocks have high wavenumber or inherent stiffness, so the error introduced by the numerical methods is relatively high.Even before applying any discretization, the error is introduced in the solution by the MOL algorithm. Let assume that we have an exact integration or differentiation schemes but still, we are far away from the exact solution because of MOL assumptions. I like to know whether any alternatives for MOL available? or any method based on the method of weighted residue approach that completely works on space-time term rather than standard FEM which works on space alone. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Unknown function type pressureTools | Dorian1504 | OpenFOAM Post-Processing | 23 | May 25, 2021 10:24 |
| problem during mpi in server: expected Scalar, found on line 0 the word 'nan' | muth | OpenFOAM Running, Solving & CFD | 3 | August 27, 2018 05:18 |
| [OpenFOAM] Take derivative of mean velocity in paraFoam | hiuluom | ParaView | 13 | April 26, 2016 07:44 |
| [OpenFOAM] Annoying issue of automatic "Rescale to Data Range " with paraFoam/paraview 3.12 | keepfit | ParaView | 60 | September 18, 2013 04:23 |
| error while compiling the USER Sub routine | CFD user | CFX | 3 | November 25, 2002 16:16 |