 |
|
|
[Sponsors] | |||||
Unequal wall-normal grid spacing and solution of pressure equation with natural bc |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Tony Zahtila
Join Date: Mar 2016
Posts: 33
Rep Power: 10  |
Hi there,
I was wondering if anyone out there had a similar experience to me regarding implementing unequal wall-normal grid spacing in the domain. Specifically, in order to solve a poisson equation with natural boundary conditions, i.e partial p/partial n = 0 at the walls, I need the sum of the source term globally to come to zero. If this isn't satisfied, the iterative solution will not converge but continue to shift by a constant. I am able to implement this for a Navier Stokes code if the domain is equally spaced but I cannot seem to achieve this with an unequal spacing in the wall-normal direction. If anyone has had this problem, please let me know of your solution. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
The pressure solution is always defined up to a function of time, if you prescribe homogeneous Neumann BCs. you must change the source term in the Poisson equation accordingly to fulfill the compatibility condition. On a non-uniform grid there is nothing different. You can read how to implement here https://www.researchgate.net/publica...uqt7Fko0rKOcng |
||
|
|

|
||
|
|
|
#3 | |
|
Member
Tony Zahtila
Join Date: Mar 2016
Posts: 33
Rep Power: 10  |
Quote:
Thanks for taking time to reply to my thread. This paper is very long, which page/section should I read? Kind regards. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
||
|
|

|
|
|
|
|
#5 |
|
Member
Tony Zahtila
Join Date: Mar 2016
Posts: 33
Rep Power: 10  |
Hi Dr. Denaro,
My concern rests in my experience that non-homogenous boundary conditions can actually effect the solution of the variable, particularly at the first grid point but also throughout the domain? I have tried solving poisson equations in 1D with arbitrary source term and found that my results w/ and w.o homongeous boundary conditions differed? Kind regards. |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
No, apart from the additive constant, the two approaches are numerically equivalent. Check for some bug in your code. |
||
|
|

|
||
|
|
|
#7 | |
|
Member
Tony Zahtila
Join Date: Mar 2016
Posts: 33
Rep Power: 10  |
Quote:
Dear Dr.Denaro, I am still a bit confused, in your paper I can see that the pressure boundary condition is, for the boundary elements, 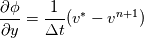 This is equation 18 on page 404 of the journal article in the paper that you have sent me. However, when I solve for the intermediate velocity field, my boundary conditions are u*,v*,w* Dirichlet zero. So doesn't that right hand side go to zero? |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
No, the intermediate velocity field at the boundaries is not prescribed to vanish. It depends on an expression that is function of the real velocity and the pressure gradient. But, no matter about the intermediate velocity, the Neumann condition is prescribed in such a way that v* will be eliminated by difference with the same term that appears in the RHS of the Poisson equation. |
|
|
|

|
|
|
|
|
#9 | |
|
Member
Tony Zahtila
Join Date: Mar 2016
Posts: 33
Rep Power: 10  |
Quote:
I am wondering why you wouldn't just set the intermediate velocity field to be zero at the boundary and then use a finite volume discretization? This will necessarily satisfy the integrability constraint? Kind regards. |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
If you see the expression of the Hodge decomposition, the only known physical condition that can be prescribed on a boundary is the natural velocity. Therefore, you know only that the difference between the intermediate velocity and the pressure gradient is a known value but nothing is known for each one of both. Setting a zero value for the intermediate velocity is misleading. I discussed many details about that in this paper https://www.researchgate.net/publica...ection_methods |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Reynolds transport, turbulence model, etc | Beginner | Main CFD Forum | 1 | January 7, 2009 06:36 |
| BC for Pressure Correction on Colocated Grid | Matt Umbel | Main CFD Forum | 1 | October 3, 2000 20:44 |
| Grid Independent Solution | Chuck Leakeas | Main CFD Forum | 2 | May 26, 2000 12:18 |
| Grid Quality and the Solution | Faraz | Main CFD Forum | 4 | January 10, 2000 19:18 |