 |
|
|
[Sponsors] | |||||
Does solenoidal field orthogonal to dilatational field? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Hi,
Currently I am reading a paper about compressible homogeneous isotropic turbulence. In this paper, the authors claim that  where <> stands for volume averaging, and superscript s & d represent solenoidal/dilatational velocity fields, which can be obtained from Helmholtz decomposition. I really don't see how this identity is valid. Solenoidal and dilatational components are orthogonal in spectral space, that's for sure. But I don't think it is equivalent to be orthogonal in physical space. Or I am misunderstanding this identity; it's equal to zero because some other reason? Can anyone give me some hints? Appreciate it. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Yes, they are not orthogonal each other in pointwise sense. The orthogonality is in the sense of the generalized inner product not in the standard inner product implied by the Pythagorean theorem. I explained this issue after Eq.(3) here https://www.researchgate.net/publica...ary_conditions |
|
|
|

|
|
|
|
|
#3 | ||
|
Senior Member
|
Quote:
1. In Case 1, Eq.(3), for the last 2 lines, how you reach final conclusion from 2nd line? 2. Under Eq.(3), you mentioned Quote:
|
|||
|
|

|
|||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
- The HHD can be seen in two ways, the second bein the case of prescribed tangential boundary condition. In practice, the well know vorticity-stream function formulation is nothing but the second case of the HHD. - If you see the surface integral it vanishes if either the normal component is zero or it is prescribed with the periodicity. In such case the integrals along two faces with opposite outward unit normal will compensate |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
|
Quote:
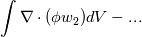 may or may not be zero. 2. See if I am correct. Let's start with your Case 2 in Eq.3. When we reach the 2nd line, i.e.,  with periodicity, the entire divergence will be zero. Correct? And so the solenoidal part will be orthogonal to the dilatational part. |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
- Case 1 has w2 that is divergence-free by definition then you convert the volume integral of the div to a surface integral of the normal flux. That is zero for periodic conditions
- The same is in Case 2, you use Gauss to convert the volume integral to a surface integral wherein you can use the prescribed BCs to assess that the integral is zero. Is that the answer you asked or I do not understand your question? |
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
|
Quote:
- I just want to be sure that I understand your Case 2-Eq.3 correctly. So, in the paper I mentioned at the very beginning, the authors claim that  where superscript s & d stand for solenoidal/dilatational components. Since you mentioned above that solenoidal/dilatational components are orthogonal in the global sense. I just want to be sure does this averaging operation count as "global"? |
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
well, generally the brackets are used as denomination of an ensemble averaging but if the paper addresses them as volume integral then the orthogonality is implied, provided that the correct BCs are associated. |
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
Yes, in the paper, it's volume averaging, and periodic BCs are applied in all directions.
|
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
|
BTW, is there any benchmark cases that I can test my HHD code? I only need cases with simple periodic BCs.
|
|
|
|

|
|
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#12 |
|
Senior Member
|
The solution to the Taylor-Green vortex?
Also, just a side question: I decompose the field in spectral space via the projection tensor  I apply this tensor on the velocity field and it gives back the solenoidal part; and then I use ifft to invert back to physical space. However, the resulting solenoidal field I got, if I take the real part of the solution, the divergence is significant, not close to zero; but if I include the complex part as well, the divergence is perfectly zero (in the sense of machine precision). But definitely the solution should be real; I am afraid if I directly throw away the complex part, the solution won't be correct. I check my code many times and I don't see any problem with it. So could you possibly give me some hint? |
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
yes, you can use the 2D or the 3D formulation of the Taylor solution. I am not sure to understand what you are doing. First, the HHD allows you to determine the gradient of the pressure, the absolute pressure function being not unique. Then, the divergence-free field is the sum of the original vector field you want to decompose and the computed pressure gradient. Could you better detail what are you doing? In spectral methods the divergence-free constraint is imposed. |
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
|
Quote:
What I am doing is following Pope (Turbulent Flows, Chp.6, Sec.4). The basic idea is doing this decomposition in spectral space. The velocity in spectral space can be decomposed into the components which parallel to the wave vector, and the other one will be orthogonal to it. The one orthogonal to the wave vector is the solenoidal velocity. To perform this decomposition in spectral space, one can do the projection of the velocity to get this orthogonal component in spectral space by (suppose  stands for the Fourier coefficients) stands for the Fourier coefficients) in which the projection tensor  is defined as is defined as where  is the wave vector components. Then can subtract the solenoidal parts from original field to get the dilatational parts. is the wave vector components. Then can subtract the solenoidal parts from original field to get the dilatational parts.My problem is homogeneous isotropic turbulence, so have periodic BCs in all 3 directions. The basic algorithm I am using is 1. Perform FFT on velocity to get its counterpart in Fourier space; 2. Doing the projection mentioned above to get solenoidal velocity field  in spectral space in spectral space 3. Subtract  from from  to get the dilatational parts to get the dilatational parts  4. Apply iFFT on  and and  to get the physical solution of solenoidal and dilatational velocity fields. to get the physical solution of solenoidal and dilatational velocity fields.But my issue is, the solenoidal field I get is a complex field; if I throw out the imaginary parts, the real parts are not exactly divergence-free; if I keep the imaginary parts, then the divergence will be machine-zero. Apparently, the solution should be real, so at some point I need to toss out the imaginary part anyway. But I am afraid if I do, the solution would not be exactly divergence-free. |
||
|
|

|
||
|
|
|
#15 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Some things are still not clear to me.
1) For compressible flow there is no divergence-free constraint, however at a steady state the mass flux rho*v is solenoidal, not the single velocity field. Are you searching for that field? 2) the pressure gradient exists always as a term in the momentum equation 3) When you consider a Fourier representation of a real function f(x), you have to sum the products of the complex numbers, that is F(k)*exp(i*k*x), over all the wavenumbers and use the property of the coefficient to be conjugate. It will result in a real function. |
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
|
Quote:
 I am not looking for some fields that is inherently divergence-free in the compressible flow. I only want to separate the velocity field. 2. Maybe I am not correct on this pressure problem. But it does not concern me right now. 3. I am not sure if I understand this response of yours. What I meant complex, is about when I evaluating the divergence of the solenoidal velocity field (after I do the decomposition) via spectral method, namely, something like  where  is the inverse Fourier transform. And then the divergence is the inverse Fourier transform. And then the divergence  Then I look at the field div, it's complex, and its real part is not exactly divergence-free. |
||
|
|

|
||
|
|
|
#17 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
du/dx+dv/dy+dw/dz = i*(kx*u+ky*v+kz*w) for real kx,ky,kz that has only the imaginary part, the real part being zero, when you set the divergence-free constraint you get a condition only on it kx*u+ky*v+kz*w=0 |
|
|
|

|
|
|
|
|
#18 | |
|
Senior Member
|
Quote:
 then inverse it to get its result in physical space, i.e.,  Then I sum each derivative up in physical space to get the divergence. Is this not the way to do it? Should I just compute the divergence in spectral space? |
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I do not understand what you are doing... the derivative is du/dx = i*kx*u where u is the real function not the Fourier coefficients! It is due to the eigenfunction property |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
|
||
|
|

|
|
 |
| Tags |
| compressible flow, dilatational, helmholtz decomposition, solenoidal |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| simpleDyMFoam on v1806 | gamemakerh | OpenFOAM Programming & Development | 0 | November 8, 2018 09:15 |
| potential flows, helmholtz decomposition and other stuffs | pigna | Main CFD Forum | 1 | October 26, 2017 09:34 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Zero size field | taranov | OpenFOAM Bugs | 2 | April 20, 2010 05:51 |
| Problem with rhoSimpleFoam | matteo_gautero | OpenFOAM Running, Solving & CFD | 0 | February 28, 2008 07:51 |