 |
|
|
[Sponsors] | |||||
Does solenoidal field orthogonal to dilatational field? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#21 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
If you start from the Fourier series expressing u(x) as sum of U(k)*exp(i*k*x) you see the definition by using a single component du/dx = U(k) d/dx exp(i*k*x) = i*k*U(k)*exp(i*k*x)= i*k*u(x) you can think about the derivative of the spectral interpolant, see https://people.maths.ox.ac.uk/trefethen/7all.pdf A clear explanation of the two approaches is provided in section 2.1.3 of the textbook https://www.springer.com/us/book/9783540307259 see also here, note 4 raised the point about the complex derivative https://math.mit.edu/~stevenj/fft-deriv.pdf However, you are working on the divergence-free function so I would use the equation like kx*U(kx)+ky*V(ky)+kz*W(kz)=0 Last edited by FMDenaro; April 11, 2019 at 12:38. |
||
|
|

|
||
|
|
|
#22 | |
|
Senior Member
|
Quote:
But come back to my previous question: after I decompose the velocity field in spectral space and inverse FFT the velocity fields back to physical space, the imaginary parts are not close to zero. I tested my HHD code on Taylor-Green vortex, it works perfectly well; so I don't think it's the issue with my HHD code. Now I am thinking could it due to aliasing? Otherwise, I don't see other possibilities. |
||
|
|

|
||
|
|
|
#23 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
when you consider the derivative, you get [i*k*U(k)]*exp(i*k*x), the term in the square brackets is the Fourier transform of du/dx, have a look at Eq.(2.6) in the Trefethen notes.
|
|
|
|

|
|
|
|
|
#24 | |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
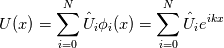 being trigonometric expansion with 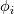 being your modal basis functions and being your modal basis functions and  are your modal coefficients (spectral). are your modal coefficients (spectral). You can also define the same polynomial in Lagrange form with 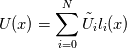 being the Lagrange expansion with  being your nodal basis functions and being your nodal basis functions and 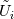 are your nodal coefficients (physical) are your nodal coefficients (physical)Here 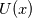 is the same polynomial in different representation. is the same polynomial in different representation.You call  the discrete Fourier-transform and the discrete Fourier-transform and 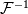 its inverse. its inverse.Formally you can write both 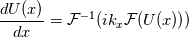 or 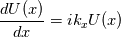 because a polynomial is a polynomial is a polynomial, or to put it another way, it is only a case of representation. Perhaps it is better to write 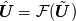 or vice versa  with ![\hat{\boldsymbol{U}}=[\hat{U}_0,\hat{U}_1,...,\hat{U}_N]^T \hat{\boldsymbol{U}}=[\hat{U}_0,\hat{U}_1,...,\hat{U}_N]^T](/Forums/vbLatex/img/ef2454017eb343ea8563e888ed9b9c32-1.gif) being the the vector of modal coefficients and ![\tilde{\boldsymbol{U}}=[\tilde{U}_0,\tilde{U}_1,...,\tilde{U}_N]^T \tilde{\boldsymbol{U}}=[\tilde{U}_0,\tilde{U}_1,...,\tilde{U}_N]^T](/Forums/vbLatex/img/ab8fba5d076dc039175e48df2d0f2c91-1.gif) being the the vector of nodal coefficients The discrete Fourier-transform only changes the coefficients. |
||
|
|

|
||
|
|
|
#25 |
|
Senior Member
|
This is how I would get the spectral derivative dy/dx of a periodic function y(x) in MATLAB for a given set of coordinates x with constant spacing:
%MATLAB SECTION nx=length(x); Lx=x(end)-x(1); y=y(1:end-1); nx=nx-1; %Remove periodicity Nc=(nx+mod(nx,2))/2-1; kx1=2*pi*(0:Nc)/Lx; kx2=2*pi*(-Nc:-1)/Lx; if mod(nx,2)==1 kx=[kx1 kx2];else kx=[kx1 0 kx2];end y_hat = fft(y); dydx_hat = 1i*kx.*y_hat; dydx = real(ifft(dydx_hat)); dydx = [dydx dydx(1)]; %Add back periodicity %END OF MATLAB SECTION where the remove and add-back periodicity are NOT needed if the end points are NOT actually the same. For example, use it for finite difference computations but not finite volume ones. |
|
|
|

|
|
|
|
|
#26 |
|
Senior Member
|
Quote:
|
|
|
|

|
|
|
|
|
#27 | |
|
Senior Member
|
Quote:
By my question was: the solution I got back from iFFT is complex, and the imaginary part is significant. I believe it's due to the aliasing errors. So I am wondering is there anyway I can separate these aliasing errors, analyze them quantitatively? |
||
|
|

|
||
|
|
|
#28 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Quote:
|
|
|
|

|
|
|
|
|
#29 | |
|
Senior Member
|
Quote:
In general, I would use a test field to see that everything works as expected, before moving to the actual data you have no control over. |
||
|
|

|
||
|
|
|
#30 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Have you checked your FFT and iFFT processes first on a known derivative? What happens if you consider a function like sin(2*pi*k/L) for several values of k? |
||
|
|

|
||
|
|
|
#31 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Have also a look to the HHD in spectral space here
http://bohr.physics.berkeley.edu/cla...amclassemf.pdf |
|
|
|

|
|
|
|
|
#32 | |
|
Senior Member
|
Quote:
And I checked the note you attached. It is the same as what I did. So, I believe the complex issue stems from the aliasing error. |
||
|
|

|
||
|
|
|
#33 | |
|
Senior Member
|
Quote:
|
||
|
|

|
||
|
|
|
#34 | |
|
Senior Member
|
Quote:
Peterson, Livescu, Forcing for statistically stationary compressible isotropic turbulence. PoF (2010). And I made a mistake; it actually should be 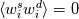 where 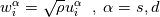 And yeah, the topic kinda drifted away.... |
||
|
|

|
||
|
|
|
#35 | |
|
Senior Member
|
Quote:
However, Taylor solution, if I recall well, is soleinodal. You should try something that is dilatational as well, if you haven't already. |
||
|
|

|
||
|
|
|
#36 | |
|
Senior Member
|
Quote:
As for the aliased field, do you happen to know any? |
||
|
|

|
||
|
|
|
#37 |
|
Senior Member
|
In 2d the taylor solution can be parameterized with respect to the wavelength. You can check my phd thesis here on my blog for it (but it is easy to derive as well). Just use a wavelength higher than what your resolution can sustain
|
|
|
|

|
|
|
|
|
#38 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
To assess if the problem is in the aliasing you should replicate a controlled test. On a grid of size h and Nyquist frequency Kc=pi/h, sample the function sin (k*x) for k<Kc and k>Kc and check the resulting FFT/iFFT for the function and derivative |
||
|
|

|
||
|
|
|
#39 | |
|
Senior Member
|
Quote:
Code:
clearvars; clc; close all N = 64; L = 2*pi; dx = L / N; x = 0 : dx : L; w = 33; y = sin(w * x); % FFT/iFFT yk = fft(y(1:end-1)); yp = ifft(yk); % derivative k = [0:N/2-1, -N/2:-1]; dydxhat = 1i * k .* yk; dydx = ifft(dydxhat); |
||
|
|

|
||
|
|
|
#40 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
"But the resulting y is practically zero"
what do you mean? I run your code at w=1,16,33 and checked the y and yp vectors and they are not zero |
|
|
|

|
|
 |
| Tags |
| compressible flow, dilatational, helmholtz decomposition, solenoidal |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| simpleDyMFoam on v1806 | gamemakerh | OpenFOAM Programming & Development | 0 | November 8, 2018 09:15 |
| potential flows, helmholtz decomposition and other stuffs | pigna | Main CFD Forum | 1 | October 26, 2017 09:34 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Zero size field | taranov | OpenFOAM Bugs | 2 | April 20, 2010 05:51 |
| Problem with rhoSimpleFoam | matteo_gautero | OpenFOAM Running, Solving & CFD | 0 | February 28, 2008 07:51 |