 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
|
Greetings,
I am trying to understand the definition of Q-criterion, which is the 2nd invariants of the velocity gradient tensor ![Q = \frac{1}{2}\left[\text{tr}(D)^2 - \text{tr}(D^2)\right] = \frac{1}{2}(D_{ii}D_{jj} - D_{ij}D_{ji}) = \frac{1}{2}(u_{i,i}u_{j,j} - u_{i,j}u_{j,i}) Q = \frac{1}{2}\left[\text{tr}(D)^2 - \text{tr}(D^2)\right] = \frac{1}{2}(D_{ii}D_{jj} - D_{ij}D_{ji}) = \frac{1}{2}(u_{i,i}u_{j,j} - u_{i,j}u_{j,i})](/Forums/vbLatex/img/130e984e915853396e312ed3adf08250-1.gif) where the  is the velocity gradient tensor. Under the incompressible condition, will reduce to is the velocity gradient tensor. Under the incompressible condition, will reduce to  Well, this part I can totally get it. But go further will have  (from Eq.(2) in [1]), where (from Eq.(2) in [1]), where 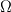 is the vorticity tensor, is the vorticity tensor, 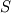 is the rate-of-strain tensor, and the magnitude is defined as is the rate-of-strain tensor, and the magnitude is defined as  . .However, if start from this one and go back to the definition stated at the top, I just can't reach the same result, which I have ![Q = \frac{1}{2}[(u_{i,j} - u_{j,i})(u_{j,i} - u_{i,j}) - (u_{i,j} + u_{j,i})(u_{j,i} + u_{i,j})] = -\frac{1}{2}(u_{i,j}u_{i,j} + u_{j,i}u_{j,i}) \neq -\frac{1}{2}u_{i,j}u_{j,i} Q = \frac{1}{2}[(u_{i,j} - u_{j,i})(u_{j,i} - u_{i,j}) - (u_{i,j} + u_{j,i})(u_{j,i} + u_{i,j})] = -\frac{1}{2}(u_{i,j}u_{i,j} + u_{j,i}u_{j,i}) \neq -\frac{1}{2}u_{i,j}u_{j,i}](/Forums/vbLatex/img/2ca5702fcda6fd9eb3bd8eaf69643475-1.gif) or  which apparently different from the one after applying incompressible condition. I am not sure where it goes wrong. So can anybody give me some hints? Thanks a lot! PS: most of the definitions come from here [1]. J.Jeong, F.Hussain, On the identification of vortex, J. Fluid Mech. (1995), vol. 285, pp. 69-94 |
|
|
|

|
|
|
|
|
#2 |
|
New Member
Shang
Join Date: Jan 2018
Posts: 5
Rep Power: 8  |
Hi,
Have you figured it out? I just drop by this post. I guess that the problem lies in the defintion of the magnitude of Omega, mag(Omega)^2=Omega(ij)Omega(ij). Then you can get the correct Q. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
|
Quote:
The definition of mag(Omega) is given in the paper. But it seems to me the one you proposed is the same as theirs. |
||
|
|

|
||
|
|
|
#4 |
|
New Member
Shang
Join Date: Jan 2018
Posts: 5
Rep Power: 8  |
Hi,
Please correct me if I am wrong. The inner product of two tensors: C(ij)=A(ik)B(kj) A(ik)=Omega(ik) B(kj)=Transpose[Omega(kj)]=Omega(jk) Then, C(ij)=Omega(ik)Omega(jk) tr[C(ij)]=C(ii)=C(jj)=Omega(ik)Omega(ik)=Omega(jk)Omega(jk) Their definition seems correct. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Shang
Join Date: Jan 2018
Posts: 5
Rep Power: 8  |
Anyway,
tr(A^2)=A(ij)A(ji) tr(AA^T)=A(ij)A(ij) The ordering in tensor calculus does make sense. |
|
|
|

|
|
 |
| Tags |
| q criterion |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| problem with Min/max rho | tH3f0rC3 | OpenFOAM | 8 | July 31, 2019 10:48 |
| Stopping criterion for outer iteration loop | luftraudi | Main CFD Forum | 3 | February 22, 2017 09:59 |
| It has to include complete definition of a type (not just fwd declaration), isn't it? | Zeppo | OpenFOAM Programming & Development | 12 | August 16, 2016 15:01 |
| (AutoGRID 5) Problem in Geometry definition of propeller | venkat_aero2007 | Fidelity CFD | 14 | July 31, 2012 15:05 |
| OpenFOAM static build on Cray XT5 | asaijo | OpenFOAM Installation | 9 | April 6, 2011 13:21 |