 |
|
|
[Sponsors] | |||||
Discontinuous Galerkin: Physical to Reference Frame transformation of 1D advection eq |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
I have a question regarding the Discontinuous Galerkin (DG) discretisation of the 1D advection equation of the form
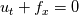 , specifically regarding the transformation from the physical to reference frame (say from x to r, i.e. from some physical element between , specifically regarding the transformation from the physical to reference frame (say from x to r, i.e. from some physical element between 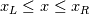 to some reference element between to some reference element between 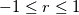 ). ).If I discretise the advection equation in strong form using the standard DG method I arrive at (in the physical frame with test function  ): ): ![\mathbf{M} u_t + \mathbf{S} f_x = \int_F n \cdot [(f-f^*)\phi(x)]\mathrm{d}x \mathbf{M} u_t + \mathbf{S} f_x = \int_F n \cdot [(f-f^*)\phi(x)]\mathrm{d}x](/Forums/vbLatex/img/fa182ea3962041fc2ec5ecbd209b852b-1.gif) , ,where 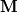 and and  denote the mass and stiffness matrix, respectively. They are given as denote the mass and stiffness matrix, respectively. They are given as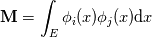 , , . .Here and in the previous equation, the subscripts E and F denote the element and its face, respectively. If I transform the above mass and stiffness matrix into reference frame, I end up with  , ,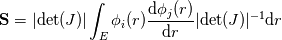 , ,where J is the jacobian due to the mapping which cancels itself out in the stiffness matrix. Now, for the right-hand side we proceed in a similar fashion, for which we can write in reference frame: ![RHS = \int_F n\cdot [(f-f^*)\phi(r)|\mathrm{det}(J)|]\mathrm{d}r RHS = \int_F n\cdot [(f-f^*)\phi(r)|\mathrm{det}(J)|]\mathrm{d}r](/Forums/vbLatex/img/1cfac72474d21bff85abdbe656b9fb00-1.gif) . .So far I am able to follow the discussion, however, when reading the book of Hesthaven and Warburton "Nodal Discontinuous Galerkin Methods", they drop the Jacobian from the right hand side, i.e. they have ![RHS = \int_F n\cdot [(f-f^*)\phi(r)]\mathrm{d}r RHS = \int_F n\cdot [(f-f^*)\phi(r)]\mathrm{d}r](/Forums/vbLatex/img/22c2143ea667dbadf538ce22f579aad5-1.gif) . .I am not quite sure how we can simplify the above expression (I am probably just missing something obvious here) so that the Jacobian vanishes (at least in 1D, as is here the case). Note: The Jacobian in the case turns out to be  and not unity, so it does not simply vanish. and not unity, so it does not simply vanish.
Last edited by t.teschner; January 8, 2019 at 10:15. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Dear Teschner,
the RHS term on the right side comes from the flux part. You miss the division of the jacobian. (see stiffness matrix part). Your first equation is no good idea to start your transformation. Regards |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
I corrected the typo in the first equation (this is the same equation as Hesthaven and Warburton use, good idea or not, I am just trying to understand why the jacobian is missing in their case).
But the division of the jacobian should come from the  part in the stiffness matrix. There is no derivative of part in the stiffness matrix. There is no derivative of 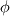 on the RHS so I am not sure how you intend to introduce the inverse Jacobian on the RHS. on the RHS so I am not sure how you intend to introduce the inverse Jacobian on the RHS.
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#5 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
Edit:
I have to correct/extend my last post. Consider the 1D case: The transformation of 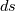 is different to is different to  in the case, that you will get different determinants. If you integrate over a surface (point) in 1D you will get the identity (=1). in the case, that you will get different determinants. If you integrate over a surface (point) in 1D you will get the identity (=1).The 2D/3D case will be different. A good explanation is given in the book of D. Kopriva " Implementing Spectral methods". In general is holds: Surface: 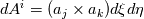 Volume: 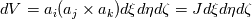 where  are the covariant metrics and are the covariant metrics and 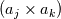 are the cross product metrics. are the cross product metrics.Regards Last edited by Eifoehn4; January 9, 2019 at 16:32. |
|
|
|

|
|
|
|
|
#6 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
I agree with your comments about the equation (I would also write it more generally as a surface integral), but, again, I am just following the notation in the book of Hesthaven and Warburton to be consistent.
Can you be more specific why in 1D the transformation of ds and dx are different (and unity for the 1D case?)? This seems to be exactly the point where I am stuck on. Or if you could point me to the section/pages in the book of Kopriva that would also help. Thanks for your help so far. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
I have to admit the 1D case is a little bit strange.
Consider the fundamental theorem of calculus which is nothing else as the divergence theorem in 1D ![\int_a^b f(x) dx = [F(x)]_a^b= F(b)-F(a). \int_a^b f(x) dx = [F(x)]_a^b= F(b)-F(a).](/Forums/vbLatex/img/62c6a6f378baf348ce23c5b2066cee51-1.gif) You can do this also for the derivative ![\int_a^b f(x)_x dx = [f(x)]_a^b= f(b)-f(a). \int_a^b f(x)_x dx = [f(x)]_a^b= f(b)-f(a).](/Forums/vbLatex/img/ad27a48990136bb252ca6d26a1d33ad0-1.gif) You can do this also for an indefinite integral 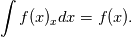 or with range  If you compare it with  you can see, that a surface integral in 1D is nothing else than the evaluation of its integral kernel at its boundaries. Your equation ![\mathbf{M} u_t + \mathbf{S} f_x = \int_{\partial E} n \cdot [(f(s)-f^*)\phi(s)]\mathrm{d}s. \mathbf{M} u_t + \mathbf{S} f_x = \int_{\partial E} n \cdot [(f(s)-f^*)\phi(s)]\mathrm{d}s.](/Forums/vbLatex/img/2ad263255bb09913819edc9cb2b2386f-1.gif) will become ![\mathbf{M} u_t + \mathbf{S} f_x = [(f -f^*) \phi]_-^+ = (f^{+} -f^{*,+}) \phi^{+} - (f^{-} -f^{*,-}) \phi^{-} . \mathbf{M} u_t + \mathbf{S} f_x = [(f -f^*) \phi]_-^+ = (f^{+} -f^{*,+}) \phi^{+} - (f^{-} -f^{*,-}) \phi^{-} .](/Forums/vbLatex/img/45a5dfc0756c1d7325d8bb7749b2d527-1.gif) with 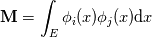  or transformed ![\mathbf{M} u_t + \mathbf{S} f_{r} = [(f -f^*) \phi]_-^+ = (f^{+} -f^{*,+}) \phi^{+} - (f^{-} -f^{*,-}) \phi^{-} . \mathbf{M} u_t + \mathbf{S} f_{r} = [(f -f^*) \phi]_-^+ = (f^{+} -f^{*,+}) \phi^{+} - (f^{-} -f^{*,-}) \phi^{-} .](/Forums/vbLatex/img/576e6ff3b46c024337915d17793d315b-1.gif) with  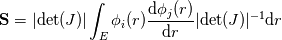 I think the answer to your question is, that the integral over 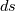 in 1D vanishes. in 1D vanishes.Kopriva page 234. Cheers |
|
|
|

|
|
|
|
|
#8 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
||
|
|

|
|
|
|
|
#9 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
Thanks for making the effort. This all makes sense and the Kopriva book also gave a good alternative view.
It doesn't explain why the Jacobian is not there (still), but I did some more reading in the Hesthaven and Warburton book, in different places they use a sort of hybrid scheme, where the left-hand side (i.e.  ) is transformed to reference frame (in the range -1 to 1) while the right hand side ) is transformed to reference frame (in the range -1 to 1) while the right hand side ![\int_{\partial E}n\cdot [(f-f^*)\phi] \int_{\partial E}n\cdot [(f-f^*)\phi]](/Forums/vbLatex/img/218f8e124abb6e46b4f983acd077cae4-1.gif) is evaluated in physical space. Not quite sure why you would do that (maybe because the polynomials are easier to evaluate in reference coordinates which does not have to be done for the right-hand side?!) but at least from a mathematical point of view the equations start to look sensible again. is evaluated in physical space. Not quite sure why you would do that (maybe because the polynomials are easier to evaluate in reference coordinates which does not have to be done for the right-hand side?!) but at least from a mathematical point of view the equations start to look sensible again. I will think about this a bit more but thanks for your help. |
|
|
|

|
|
|
|
|
#10 |
|
Senior Member
Tom-Robin Teschner
Join Date: Dec 2011
Location: Cranfield, UK
Posts: 211
Rep Power: 17  |
so it seems the answer was easier than I thought, and we are probably talking about the same thing, just in different ways. the detail I overlooked is that in 1D the volume integral is a line (so it has a jacobian) but the surface integral is a point (so it doesn't have a jacobian) ...
|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
-
Join Date: Jul 2012
Location: Germany
Posts: 184
Rep Power: 14  |
And it is even easier. Not only the jacobian vanishes. Formally you simply have no integral for RHS in 1D.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Setting the height of the stream in the free channel | kevinmccartin | CFX | 12 | October 13, 2022 22:43 |
| It would be wonderful if a tool for FoamToTecplot is available | luckyluke | OpenFOAM Post-Processing | 165 | November 27, 2012 07:54 |
| Question about N-S eqs. in body fixed noninertial reference frame | doctorWho | Main CFD Forum | 0 | July 12, 2011 19:07 |
| Building OpenFoAm on SGI Altix 64bits | anne | OpenFOAM Installation | 8 | June 15, 2006 10:27 |
| Windows Installation BugsComments on Petrbs patch | brooksmoses | OpenFOAM Installation | 48 | April 16, 2006 01:20 |