 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Nov 2018
Posts: 10
Rep Power: 7  |
Hello everybody.
I am quite new to the fluid dynamics world and I am currently facing a problem, which I do not understand. By following the passages done on some papers and books, I have to derive the general depth-averaged flow equations in a layer of fluid. I am using the incompressible, three-dimensional Reynolds-Averaged Navier-Stokes equations for the atmospheric boundary layer (which I do not report here since not directly related to what I do not understand). The notation used is as follow: - 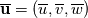 - the bar denotes that the quantity is averaged over time The first passage I do not understand is the following: ''Consider now a layer of fluid between two pliant surfaces 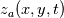 and and 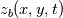 that follow a streamline, for which: that follow a streamline, for which: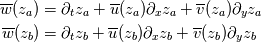 What does it mean? Which is the path that brings to these formula? Which physic interpretation can be done? The second passage I do not understand is the following: ''Since 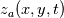 and and 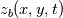 lie on a streamline, then: lie on a streamline, then: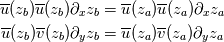 I simply do not understand why these quantities are equal. Thank you in advance for the help. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Please, link the original textbook you are using
|
|
|
|

|
|
|
|
|
#3 |
|
New Member
Join Date: Nov 2018
Posts: 10
Rep Power: 7  |
Unluckily it is written on a paper that is still not published, so I do not think that I can post it here. But anyway, what I do not understand are exactly that two passages, and in the papers they are reported with these words, no more explanation.
I did search on books or other materials, but I do not find nothing similar. Like I said, I am speaking about a layer of fluid between two pliant surface, 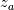 and and 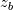 , and then that equations just pop up. , and then that equations just pop up.Whatever kind of help is appreciated, thank you. |
|
|
|

|
|
|
|
|
#4 |
|
New Member
Join Date: Nov 2018
Posts: 10
Rep Power: 7  |
Hi guys,
I did solve all problems, it was all about mathematics and some physic assumption. By the way, I have another question. What does it really mean depth-averaged flow equations? Because I am working with a model that deals with atmospheric boundary layer; this is split in three levels, and in each level there are different 3-D Navier-Stokes equations. Then it is made a depth averaged over the depth of each level, and the system becomes 2-D. Does this means that in each level all quantities along the z-direction are constant since we have averaged it? Probably it is like this, but to me it seems a very strong assumption. |
|
|
|

|
|
|
|
|
#5 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
I think that the hypothesis is that the contribution along the depth is disregardable. Maybe you can find the answer here https://coast.nd.edu/jjwteach/www/ww...s/topic1_5.pdf |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| [snappyHexMesh] SnappyHexMesh - no layer added | bejbro | OpenFOAM Meshing & Mesh Conversion | 5 | February 1, 2020 21:05 |
| [snappyHexMesh] Surface triangulation using snappyHexMesh | shaileshbg | OpenFOAM Meshing & Mesh Conversion | 4 | October 17, 2019 05:42 |
| [Gmsh] Error : Self intersecting surface mesh, computing intersections & Error : Impossible | velan | OpenFOAM Meshing & Mesh Conversion | 3 | October 22, 2015 12:05 |
| [snappyHexMesh] Layers don't fully surround surface | EVBUCF | OpenFOAM Meshing & Mesh Conversion | 14 | August 20, 2012 05:31 |