[selig5576]

If we assume an implicit formulation for LES (the SGS tensor dissipates in the same manner as the leading order error of the numerical scheme) are only certain eddy viscosity closures usable?

For example, in the dynamic model of Germano, I do not understand how one can use this model without the explicit use of the filter. When calculating C_s with the dynamic model we have an expression (resolved stress): L_ik = \tilde{\bar{u}}_i \tilde{\bar{u}}_k - \tilde{\bar{u}_i \bar{u}_k}. In an implicit formulation the difference is not obvious as in practice the \bar term is not directly implemented.
Sorry if this question is naive and/or does not make sense.

[FMDenaro]

Originally Posted by selig5576

If we assume an implicit formulation for LES (the SGS tensor dissipates in the same manner as the leading order error of the numerical scheme) are only certain eddy viscosity closures usable?

For example, in the dynamic model of Germano, I do not understand how one can use this model without the explicit use of the filter. When calculating C_s with the dynamic model we have an expression (resolved stress): L_ik = \tilde{\bar{u}}_i \tilde{\bar{u}}_k - \tilde{\bar{u}_i \bar{u}_k}. In an implicit formulation the difference is not obvious as in practice the \bar term is not directly implemented.
Sorry if this question is naive and/or does not make sense.

The Germano procedure requires always to use explicitly a filtering operation (test filtering) on the velocity field. This latter field is actually a result of an implicit filtering due to the discretization.
In the hypothetical case you are using an explicit filtering formulation, you have two different filtering procedure, one for the main filtered variable u_bar and the second for the test-filtered variable (u_bar)_tilde. This latter has a greater filter width

[sbaffini]

Bar is what you resolve for, which might or not imply an explicit filter (for implicitly or explicitly filtered LES, respectively). Tilde is needed in the dynamic procedure and it necessarily needs an explicit application of a filter to bar, no matter what.

[sbaffini]

The issue you arise is actually present for scale similar models, when written using only one filter level. Those models are indeed only applicable in explicitly filtered LES.

[selig5576]

Thank you for the replies! For implicit LES, as far as I can see, the static Smagorinsky is the only algebraic model that one can use in implicit LES, is that correct?

If that is the case, how do the users of ILES take into account the fact that the Smagorinsky model has trouble handling free-shear flows?

[sbaffini]

As the topic is per se confusing, it is of paramount importance using the correct nomenclature to avoid further confusion. In this regard:

- Implicit LES (ILES): An LES performed without any SGS model at all. Also known as coarse DNS, this typically requires certain numerical schemes to actually have a practical sense. By contrast, explicit LES is any LES with a SGS model, no matter of what kind.

- Implicitly filtered LES: an LES where no actual filtering is applied on the governing equations (or just the convective terms, depending on the formulation) in order to obtain the solved variables themselves. This basically is like running an URANS code (or a laminar code) with a SGS model (no matter of what kind). Nonetheless, an explicit filter can still be applied in order to derive variables used in the SGS model (like in the Germano dynamic procedure, or some form of scale similar models). This is the most common approach in use today.

- Explicitly filtered LES: at each time step you apply a numerical filter on some terms of the equations before going to the next time step. Any other filter (e.g., in the dynamic procedure) is on top of this. Mostly used at academic level (and probably just sometimes at stanford CTR).

With this distinction, I guess you were actually referring implicitly filtered LES, the most common approach today. You can use, in pratcice, any SGS model with it. In this case the bar variables are just the variables you solve the equations for. You can't, in this framework, have a double bar variable, but you can have tilde applied to var, hat applied to tilde applied to bar, etc..

That is, you just need to avoid an explicit application of bar (which you don't know, because is implicit in your discretization). You can do anything else.

Take a look to the first chapters of my thesis (https://www.cfd-online.com/Forums/bl...hesis-les.html), maybe it can clarify some doubts

[selig5576]

First off, thank you for devoting time to such a helpful reply. Secondly, your PhD thesis is exactly what I was looking for to clear things up. My course on turbulence at my university used Pope, and everything was reasonably clear up until we got to LES. After the section on LES it left me confused.

[FMDenaro]

Paolo provided a good framework of the several LES nomenclatures. They can sometimes had a confusing impact on a newcomer in LES field.
The term explicit/implicit can be used to both the concept of filtering and that of SGS modeling. For example, commonly ILES is an implicit-based filtering LES with an implicit SGS model induced by the local truncation error. In principle, you could also performe ILES with an explicit filtering on the convecti terms but ILES is only a "no explicit SGS model".

[sbaffini]

To be more clear, imagine running a laminar code with an LES grid.

Without doing anything else you are formally doing an implicit LES or ILES.

If you add a SGS model, say, a static Smagorinsky, you are doing an implicitly filtered LES.

In both cases, the variables you are solving the equations for are the bar ones.

Now imagine applying a numerical filter to your variables (which, I recall, are the bar ones) after each time step. It is a numerical routine that actually filters your variables. Denote this filter as tilde. After such procedure you also obtain tilde_bar variables which, in this implicitly filtered framework, you can use for a SGS model, like a dynamic smagorinsky or a certain form of scale similar model.

In case you want to use a dynamic scale similar model or a dynamic mixed model you will have to apply an additional filter, say, hat, to your tilde_bar variables, finally obtaining hat_tilde_bar variables to use in your SGS model.

[sbaffini]

Originally Posted by FMDenaro

Paolo provided a good framework of the several LES nomenclatures. They can sometimes had a confusing impact on a newcomer in LES field.
The term explicit/implicit can be used to both the concept of filtering and that of SGS modeling. For example, commonly ILES is an implicit-based filtering LES with an implicit SGS model induced by the local truncation error. In principle, you could also performe ILES with an explicit filtering on the convecti terms but ILES is only a "no explicit SGS model".

Yes, I tought that citing also an explicitly filtered ILES was clearly too much

[FMDenaro]

Originally Posted by sbaffini

Yes, I tought that citing also an explicitly filtered ILES was clearly too much

As you know, using a FV method for ILES you get into a further ambiguity: the surface integral of the convective flux is a numerical explicit filtering you are applying....

[selig5576]

I thought I would post in this topic as it is relevant to the discussion. Within the framework of an implicit filtering procedure when we consider the test filter as defined by Germano (test filter is ~ 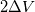). In a finite volume formulation the test filter is defined as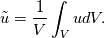



This can be approximated by (only considering the x direction)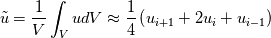



In an implementation perspective, I would have Filterx, Filtery, and Filterz. Is this a sufficient approximation to start off with? I have implemented the static Smagorinsky, and while I get good results (comparing to papers), I am looking to implement a more robust SGS model. The static Smagorinsky model I am finding to have troubles handling transition.

EDIT: I have also implemented the WALE model which gives me better results, but it does not handle free shear flows as well as the dynamic Smagorinsky. My ultimate goal is to study free shear flows.

[FMDenaro]

No, what you wrote is not correct. First, what about your grid-filtered variable? It is a FD, FV or SM approach?


For example, if you are using a FD method with second order central formula, you could consider that the grid filter variable has implicit width Delta=2h. As a consequence, the test-filtering needs a wider filter width, for example Delta_test=2*Delta=4*h.

[selig5576]

It is a second-order central FVM (although structured grid so it has the same appearance as FDM.)

In terms of constructing such that it has 4h, I think performing a volume averaging of u should be sufficient?

[FMDenaro]

Originally Posted by selig5576

It is a second-order central FVM (although structured grid so it has the same appearance as FDM.)

In terms of constructing such that it has 4h, I think performing a volume averaging of u should be sufficient?

The formula using the nodes i-1,i,i+1 does not produce a volume integral over a width 4h.
You need to discretize this integral





1/(4*h) Int[xi-2*h,xi+2*h] u_bar dx

[selig5576]

Yes. I get a filter, using Simpson's rule,



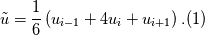In terms of applying the filter, if we consider the term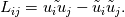



I would first apply the filter in the x direction then y and z directions. The alternative is to make a 3D filter by formulating a 3D simpsons rule, but I think this would be more difficult. Although doing this would be more aligned with the finite volume method. Thanks for all the help.

[FMDenaro]

Originally Posted by selig5576

Yes. I get a filter, using Simpson's rule,



If we consider the term



My thought is I would first apply the filter in the x direction then y and z directions given this term has no direction bias. Thanks for all the help.

No, if you consider the (1), that is the discretization of the integral over a width 2h not over 4h.

Then, if you consider the 2D extension, you can approximate it by factorization along x and z but there are formulas for a fully multidimensional integral, see for example in the book of Peric & Ferziger.

[selig5576]

You are correct. Since we need 4h, if my calculations are correct I get



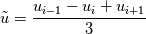In terms of how I got to this I have been following the book by Kajishima. In the example they give it is for 2 dx, but I simply used 4 dx and arrived at the above expression. I do see Ferziger and Peric have fully 2D representations.

[FMDenaro]

What you are doing is to write the differential-based filtering, that is a second order approximation based on the Taylor expansion. This formula is quite poor in terms of spectral resolution. Better results are obtained using high order derivatives. Consider also that Delta is not exactly known and Delta=2*h is an approximation for the 1D case.
I suggest to discretize the integral.



Have a look to sec. 4.1 in https://www.researchgate.net/publica...dy_Simulations


and some comments in
https://www.researchgate.net/publica...gorinsky_model


https://www.researchgate.net/publica...ied_turbulence

[selig5576]

The things I have yet to learn . I will go the integral based approach as it will end up being easier in terms of coding (don't have to do any approximate factorizations.)