[foadsf]

I have also posted my question here in StackExchange and also my code here in this GitHub Gist.


I'm trying to follow this post using Mathematica to solve Navier-Stokes equations for a compressible viscous flow in a 2D axisymmetric step. The geometry is in the attachment. Defining variables, geometry and meshing:

lc = 0.03;
rc = 0.01;
xp = 0.01;
c = 0.005;
rp = rc - c;
lp = lc - xp;
T0 = 300;
eta0 = 1.846*10^-5;
P1 = 6*10^5 ;
P0 = 10^5;
cP = 1004.9;
cnu = 717.8;
R0 = cP - cnu;

Omega = RegionDifference[Rectangle[{0, 0}, {lc, rc}], 
   Rectangle[{xp, 0}, {xp + lp, rp}]];

Needs["NDSolve`FEM`"];
mesh = ToElementMesh[Omega, "MaxBoundaryCellMeasure" -> 0.00001, 
   MaxCellMeasure -> {"Length" -> 0.0008}, 
   "MeshElementConstraint" -> 20, MeshQualityGoal -> "Maximal"];

Where the model is axisymmetric around the x axis, the governing equations including conservation equations of mass, momentum and heat can be written as: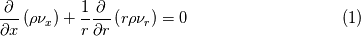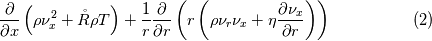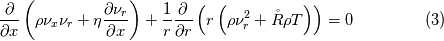





forth equation is big so I add it as a image in the attachments. Implementing the equation is Mathematica:

eqn1 = D[rho[x, r]*nux[x, r], x] + D[r*rho[x, r]*nur[x, r], r]/r == 0;
eqn2 = D[rho[x, r]*nux[x, r]^2 + R0*rho[x, r]*T[x, r], x] + 
    D[r*(rho[x, r]*nux[x, r]*nur[x, r] + eta0*D[nux[x, r], r]), r]/
     r == 0;
eqn3 = D[rho[x, r]*nux[x, r]*nur[x, r] + eta0*D[nur[x, r], x], x] + 
    D[r*(rho[x, r]*nur[x, r]^2 + R0*rho[x, r]*T[x, r]), r]/r == 0;
eqn4 = cnu*
     rho[x, r]*(nux[x, r]*D[T[x, r], x] + nur[x, r]*D[T[x, r], r]) + 
    R0*rho[x, r]*
     T[x, r]*(D[nux[x, r], x] + 
       D[r*nur[x, r], x]/r) + (2*D[nux[x, r], x]^2 + 
       2*D[nur[x, r], r]^2 + (D[nux[x, r], r] + 
          D[nur[x, r], 
           x])^2 - ((D[nux[x, r], x] + D[r*nur[x, r], x]/r)^2)*2/3)*
     eta0 == 0;
eqns = {eqn1, eqn2, eqn3, eqn4};

And the boundary conditions are:

1. constant pressure at inlet
2. constant pressure at outlet
3. axis of symmetry
4. no slip

Implemented in Mathematica as:

bc1 = R0* rho[0, r]*T0 == P1;
bc2 = R0 *rho[lc, r]*T0 == P0;
bc3 = DirichletCondition[{nur[x, 0] == 0, D[nur[x, r], r] == 0, 
    D[nux[x, r], r] == 0, D[rho[x, r], r] == 0, D[T[x, r], r] == 0}, 
   r == 0 && (0 <= x <= xp)];
bc4 = DirichletCondition[{nur[x, r] == 0, 
    nux[x, r] == 
     0}, (0 <= r <= rp && x == xp) || (r == rp && 
      xp <= x <= xp + lp) || (r == rc && 0 <= x <= lc)];
bcs = {bc1, bc2, bc3, bc4};

And then I tried to solve them by:

{nuxsol, nursol, rhosol, Tsol} = 
 NDSolveValue[{eqns, bcs}, {nux, nur, rho, T}, {x, r} \[Element] mesh,
   Method -> {"FiniteElement", 
    "InterpolationOrder" -> {nux -> 2, nur -> 2, rho -> 1, T -> 1}, 
    "IntegrationOrder" -> 5}]

But I get two errors:

NDSolveValue::femnonlinear: Nonlinear coefficients are not supported in this version of NDSolve.

And

Set::shape .... are not the same shape

So My questions are:

1. How I resolve those issues in Mathematica? Do I have any syntax errors leading to these issue? If the method/solve I'm using is not able to solve the problem then what other options do I have in Mathematica?
2. Are my equations and boundary conditions correct for the problem I'm intended to solve?
3. What other softwares can you suggest me to solve these equations? I prefer open source so I can compile and run them on a remote cluster we have in the university.