 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Senior Member
|
say, for the most common hyperbolic equation
![\partial_{t}u + \partial_{x}[f(u)] = 0 \partial_{t}u + \partial_{x}[f(u)] = 0](/Forums/vbLatex/img/f8ab42a2f6538aafaec5926b85c1a035-1.gif) Let's be specific, say 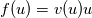 (it's the LWH traffic model) where the 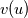 is a function of u, which is is a function of u, which is 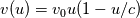 and the and the 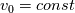 , u is the density of car flow. , u is the density of car flow.To solve this equation, of course I have to find out the CFL condition, but for the conservative form, the coefficient in front of convective term is 1 which means dt is bounded by 1; however it seems the "wave velocity" should be  which aka phase velocity. But this requires to use the product rule of the derivative and it kind of like break the conservative form and it becomes which aka phase velocity. But this requires to use the product rule of the derivative and it kind of like break the conservative form and it becomes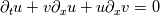 , , and now the velocity used for computing CFL should be v. But when actually solve this equation, should I back to the conservative form, or just stay with the one after product rule? And a more general question: for conservative form, how should I determine the CFL condition? What if I have a complex f(u) and not sure which one is the velocity I should use for CFL condition? Is it still the phase velocity I mentioned above? or is it something else? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
When you consider d/dx f(u) = df/du *du/dx you express the quasi-linear form of the conservation law
du/dt + f'(u) du/dx =0 Have a look to the traffic flow equation problem described in the book of Leveque (page 203). |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
|
Thx for the recommendation. I ran through the section, what I get is that, we can only determine the time step size by taking the quasi-linear form of hyperbolic equation; but when we are trying to solve the equation itself, we typically go back to the conservative form...
|
|
|
|

|
|
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#5 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
|
|
|
#7 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#8 |
|
Super Moderator
|
Yes, f'(u) is the local wave speed.
|
|
|
|

|
|
|
|
|
#9 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
||
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Problem with Velocity Poisson Equation and Vector Potential Poisson Equation | mykkujinu2201 | Main CFD Forum | 1 | August 12, 2017 14:15 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 07:27 |
| what is form of momentum equation in case of cavitation in nozzle & how it is solved | arindamsantra7 | Fluent Multiphase | 0 | August 11, 2014 04:32 |
| Conservative form and non-conservative form of NS | ARohit | Main CFD Forum | 1 | March 11, 2013 08:57 |
| Replace periodic by inlet-outlet pair | lego | CFX | 3 | November 5, 2002 21:09 |