 |
|
|
[Sponsors] | |||||
Why decreasing time step makes diffusion more significant for diffusion equation? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
I am trying to solve a simple diffusion equation
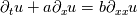 where a & b are some given constant, for the sake of simplicity, let's say they are both 1, and the spatial domain is [-1, 1] with periodic BC, the initial condition is numerical delta function 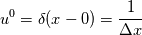 . . Solving this by simply using a naive schemes: 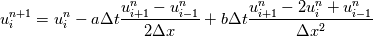 When I compare results from different time step sizes, the smaller the time step size, the more diffusive it appears to be: the wave, or the delta function, spreads out much faster in space (smoothed out) when advance in time, with smaller time step size. But according to the scheme, lowering time step size 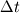 will obviously reducing the 2nd-order derivative, i.e., the diffusion term, as well, thus it should have lead to less diffusion for smaller will obviously reducing the 2nd-order derivative, i.e., the diffusion term, as well, thus it should have lead to less diffusion for smaller 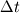 . .So where does this conflict come from? Thx! 
Last edited by TurbJet; February 15, 2018 at 15:48. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Well, there are some issues to discuss. First, look at the local truncation error of your discretization:
LTE=-0.5*dt*(a^2*d2u/dx^2-2*a*b*d3u/dx^3+b^2*d4u/dx^4) +... and, I am right, you have a higher order term in the form dx^3/dt (try to develop the LTE). Therefore, for fixed dx and vanishing dt you should get an increasing in the error. This is due to the fact that you need convergence for dx and dt going both to zero. Second, you cannot use a Dirac initial function to test such PDE as it is a non regular function. |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
|
Quote:
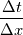 , which still leads to decreasing with smaller , which still leads to decreasing with smaller 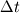 . Maybe some minor mistake in it? . Maybe some minor mistake in it?
|
||
|
|

|
||
|
|
|
#4 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
I wrote only the term of O(dt), of course you have also terms of O(dx^2). The LTE is determined by substituting the Taylor expansion in time and space in your FTCS scheme. You can do it by hand, is a bit long to manage, or you can use Maple. However, you cannot use the Dirac as initial condition and the study of the convergence requires to use dt/dx->0 |
||
|
|

|
||
|
|
|
#5 | |
|
Senior Member
|
Quote:
Anyway, I wrote out the formula for LTE only with leading order terms (probably some mistakes in those coefficients): 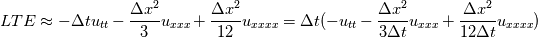 so by lowering the time step size, the LTE for time derivative would not increase, but the LTE for spatial derivative will. So which means it will increase the spatial error, and it appears to be like diffusion. Am I correct? |
||
|
|

|
||
|
|
|
#6 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
As you see, if dx is taken constant while dt is diminished, you have both a dispersion and dissipation effects. However, you should still expand d2u/dt^2 using the PDE equation
|
|
|
|

|
|
|
|
|
#7 | |
|
Senior Member
|
Quote:
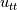 using the PDE equation"? Do you actually mean by using the PDE equation"? Do you actually mean by 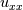 instead instead 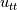 ? ?
|
||
|
|

|
||
|
|
|
#8 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#9 |
|
Senior Member
|
||
|
|

|
|
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Again, you see that using the Taylor expansion requires the solution to be regular...
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
|
Um, theoretically speaking, yes. But when I actually ran it with discretized form of Dirac function, in this case, 2/dx, it did not show some wired behavior aside from strong diffusion....
|
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Also from a numerical point of view, on a grid of size h the smallest wavelength you can represent is 2*h and that requires to describe a sine by using at least three grid points. |
||
|
|

|
||
|
|
|
#15 | |
|
Senior Member
|
Quote:
I have been trying to manage all the terms, and here is what I get 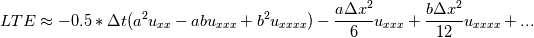 but it seems the 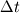 only affect those terms in the brackets; can't see any terms in the form of only affect those terms in the brackets; can't see any terms in the form of 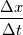 I am confused again... |
||
|
|

|
||
|
|
|
#16 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I should check all the procedure, I remember some further terms...
|
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
I checked in my old notes and I extracted the LTE expression, it appears clearly that, provided that the dx allows to get the Reynolds cell number <=2, you have a global positive diffusion coefficient.
Now the issue is that if you compare the solution at some time T, when you decreases the time step you need more iteration to reach that time and the error effects summ. |
|
|
|

|
|
 |
| Tags |
| diffusion equation, time step size |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| pressure in incompressible solvers e.g. simpleFoam | chrizzl | OpenFOAM Running, Solving & CFD | 13 | March 28, 2017 06:49 |
| simpleFoam error - "Floating point exception" | mbcx4jc2 | OpenFOAM Running, Solving & CFD | 12 | August 4, 2015 03:20 |
| Help for the small implementation in turbulence model | shipman | OpenFOAM Programming & Development | 25 | March 19, 2014 11:08 |
| Micro Scale Pore, icoFoam | gooya_kabir | OpenFOAM Running, Solving & CFD | 2 | November 2, 2013 14:58 |
| How to write k and epsilon before the abnormal end | xiuying | OpenFOAM Running, Solving & CFD | 8 | August 27, 2013 16:33 |