 |
|
|
[Sponsors] | |||||
On the diffusion term discretization on unstructured grids |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
|
Dear all,
I have a couple of doubts about the diffusion term discretization on unstructured grids. They are more philosophical than practical (and in a certain sense they are not practical at all), but I am unable to find consistent or sufficient information in the available literature, and I would like to hear from you. Here is the matter. Let us consider the generic contribution of a scalar diffusion term on the face of a finite volume cell: 1)  where  and and  are the cell face area and normal, are the cell face area and normal,  is the diffusion coefficient on the face and is the diffusion coefficient on the face and  is the gradient on the face, with the last two evaluated at the face centroid. is the gradient on the face, with the last two evaluated at the face centroid.My first doubt is about the evaluation of  . Note that, in general, such coefficient might be a function of several fields, some of which might have a gradient (e.g., density), some others might not (e.g., turbulent viscosity). . Note that, in general, such coefficient might be a function of several fields, some of which might have a gradient (e.g., density), some others might not (e.g., turbulent viscosity).In the literature, there is no clear description of the way of computing  in general. The only textbook where I found a consistent treatment is the one by Blazek; still, he suggests the simple relation: in general. The only textbook where I found a consistent treatment is the one by Blazek; still, he suggests the simple relation:2)  where L and R denotes the cell centers on the left and right of the face f. Even this simple relation, however, can be interpreted in different ways. Imagine that  , where a and b are two fields you would store in your code in any case. Then, you might not want to store also , where a and b are two fields you would store in your code in any case. Then, you might not want to store also  and have two options for it on the face (according to the previous relation). The first one is: and have two options for it on the face (according to the previous relation). The first one is:3)  But, another possibility is: 4)  Some authors suggest linear interpolation to the face, but don't provide any relation for the general unstructured case. Finally, for strongly varying properties, it is usually suggested an harmonic mean, as a result of an equivalent diffusivity. In this case, while an extension to the unstructured case is still not evident, one might argue that, following the 1D equivalent diffusivity reasoning, it makes sense to perform the (weighted) harmonic mean considering only normal to the face distances from the cell centers (i.e., like if the cell face was an infinite plane dividing the two semispaces with different properties). Long story short, for variable diffusivities, none of these seems to actually provide full second order accuracy on general unstructured grids. Thus, while I prefer to use relation 4 for simplicity, I was wandering if a clear winner exists in this case. My second doubt concerns the gradient term in (1). In the most common scenario, the whole  term is usually discretized as follows: term is usually discretized as follows:5) ![D_f = A_f \Gamma_f \left[ \left(\frac{\phi_R - \phi_L}{ds} \right) \left(\frac{1}{n_k e_k}\right) + \overline{\frac{\partial \phi}{\partial x_j}}\left(n_j - \frac{e_j}{n_k e_k}\right)\right] D_f = A_f \Gamma_f \left[ \left(\frac{\phi_R - \phi_L}{ds} \right) \left(\frac{1}{n_k e_k}\right) + \overline{\frac{\partial \phi}{\partial x_j}}\left(n_j - \frac{e_j}{n_k e_k}\right)\right]](/Forums/vbLatex/img/67f884f8dd084a1abfec0a3d89ba84a0-1.gif) where  is the versor along the segment connecting the L and R cell centers, is the versor along the segment connecting the L and R cell centers,  is the length of such segment and: is the length of such segment and:6)  My doubt is about which gradient should enter into equation (6). Typically, in unstructured codes one computes a first gradient, let's call it G, from straightforward application of Green-Gauss theorem or Least Squares approach. However, 2nd order convection schemes can't directly use G, as it might produce over/under-shoots in reconstructed face variables. So, a new gradient is produced, let's call it RG, which is a limited version of G used for 2nd order convection schemes. Until today, I did not pay too much attention to which gradient should go into equation (6) and I just used G (also because I couldn't achieve convergence with RG). This is also in line with most of the literature. However, I just realized that most papers from the Fluent developers mention something different. What they seem to use as gradient in (6) is still a new gradient, let's call it DG, built via Green-Gauss theorem, but using RG to reconstruct face values (Green-Gauss formula for gradients is based on variables on faces). On a second tought this actually makes sense in terms of consistency, as now all the face variables in the algorithm are based on the gradient RG (even if, in terms of storage, this seems to be a nightmare). What are your experiences on this? Does this really make a difference? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Paolo, maybe you know I worked years ago on unstructured 2D grid and I found any technique in the literature congruent for at the best a second order accuracy. That is totally congruent also the the FV approach where the averaged value is a second order approximation of the point-wise one.
In this framework, I think that all the approaches you described are equivalent as you wrote from the start the gradient multiplied by the area that means you are considering an averaged gradient not the real integral of the gradient. In a paper, I proposed a higher accuracy approach where the gradient is really integrated over the faces. In a simple 2D case, on a triangular grid, you have Int[Pk,Qk] nk.(Gamma*Grad phi) dSk where k goes over the total number of flux sections having Pk,Qk as initial and ending points, respectively. When you define the law y=yk(x) you can integrate Gamma(x,y(x))*Grad phi(x,y(x)). Of course, you have to represent a function from the discrete fields and on triangular grid is quite straightforward to use the shape functions in a FEM manner. A software like Maple can allow to implement in a symbolic way this approach and get the Fortran (or C) subroutine. In a 3D case you have some more work to done but the idea can be the same. Therefore my conclusion is: if you are developing a second order code, don't worry so much .... |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I can add an addition point of concern. The gradients that are being assembled per-cell in the FV scheme are based on neighbor cells without regard to cell diffusivity. Whether you use Gauss or Least Squares, you are still building linear approximations (either to the faces or across the neighborhood of the cells) and that is simply wrong for problems with significant cell-to-cell diffusivity variants. I ran into these problems over a decade ago while working on a 3D electrical model in FV where conductivity could change by several orders of magnifude from cell-to-cell. I worked in some iterative corrections to the gradients to try to account for that, but it was ugly. Of course, then the linear system it generated was a lot of fun to solve too.
So, I think your concerns are spot on. FV works well for most cases, but most of those cases don't exhibit diffusion-dominated physics. As the years pass, I am increasingly convinced of the value of DG over FV simply because issues like these can be addressed more rigorously. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
I immagine the LES case, where the requirement of an accurate discretization of the diffusive SGS flux on non regular grids should be fulfilled.
|
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
||
|
|

|
|
|
|
|
#6 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
I should point out that the Reconstruction Gradient (*_RG) fields have the convective limiters applied to them. The Gradient (*_G) fields are the unlimited gradients. There is no rationale for using limited gradients in diffusion calculations. All of the limiting schemes are applied in order to insure convective monotonicity. There is no similar principle to apply to diffusion.
My concerns about the treatment of the gradient computation and application to the diffusion flux, of course, remain. |
|
|
|

|
|
|
|
|
#7 |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,290
Rep Power: 34   |
Here are my few cents for what they are worth.
1. About the diffusion coefficients, harmonic mean is usually preferred as pointed out. One can use distance based linear interpolation. IF the calculation of diffusion coefficient is very important to calculation then one shall compute the gradients of it and reconstruct it on the face (make average of reconstructed value from both sides). This off course is costly and thus avoided. 2. The same goes for gradients at the face that are needed for diffusion term. I use linear interpolation in FVUS-Wildkatze. Many people just use average of it. |
|
|
|

|
|
|
|
|
#8 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,290
Rep Power: 34   |
Quote:
last 3 weeks I spent implementing third order flow solver in FVUS-Wildkatze and it was quite a learning experience for me. I found few things that surprised me. I am trying to create small note outlining the error differences from discretization. I will show it once done. Anyway, since in third order solver i have gradients of gradients available, i reconstruct the gradients on the face (integration points) and calculated the diffusion terms. This made huge difference in discretization error. The surprising thing that i found out that third order solver is very much less affected by the grid skew etc while second order solver is heavily affected by skew. For LES on unstructured grid it seems there are few things one can borrow from third order solver (if not the full procedure) and make the calculations better. |
||
|
|

|
||
|
|
|
#9 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
A great difference is if you perform LES on unstructured grid using the discretization as implicit filtering or using an explicit filtering.. |
||
|
|

|
||
|
|
|
#10 | |
|
Senior Member
Arjun
Join Date: Mar 2009
Location: Nurenberg, Germany
Posts: 1,290
Rep Power: 34   |
Quote:
long way for LES :-D At the moment only trying with laminar flow. For now gradient limiters are skrewing up most of the accuracy, I need to find a way to do this gradient limiting. |
||
|
|

|
||
|
|
|
#11 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Well, long way but possible...

|
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
|
Wow, that's a response, thank you all.
@Filippo: I don't know if I understand your first point. Very roughly, you say: whatever you do is correct, because you are dealing with a face averaged value, not the point value in the face centroid. But, my doubt is, wouldn't I be using in all cases (except the simplest ones) a simple first order approximation of such face averaged value? @Michael: yes, indeed, you have a point: if the gradient stencil crosses a discontinuity than I have much bigger problems than these. Either multimaterial interfaces or shock waves seem to have the same crux here. For what concerns the G-RG issue, I totally agreed with you (and somehow I still do), until I read again some papers. Let me summarize some excerpts: - The gradients used in the diffusion terms are computed using the reconstructed face values 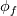 - Mathur and Murthy, Pressure Boundary Conditions for Incompressible Flow Using Unstructured Meshes, Numerical Heat Transfer B, 1997 - Mathur and Murthy, Pressure Boundary Conditions for Incompressible Flow Using Unstructured Meshes, Numerical Heat Transfer B, 1997- The cell derivatives used for the secondary diffusion terms in Eq. 12 are computed by again applying the divergence theorem over the control volume and using the averaged reconstructed values at the faces - Mathur and Murthy, A Pressure Based Method for Unstructured Meshes, Numerical Heat Transfer B, 1997 - The cell derivatives needed to evaluate  in the secondary diffusion term of equation 23 are computed by applying the Gauss theorem again over the cell control volume using the reconstructed face values as follows. - Kim, Mathur, Murthy and Choudhury, A Reynolds-Averaged Navier-Stokes Solver Using Unstructured Mesh-Based Finite-Volume Scheme, AIAA 98-0231 in the secondary diffusion term of equation 23 are computed by applying the Gauss theorem again over the cell control volume using the reconstructed face values as follows. - Kim, Mathur, Murthy and Choudhury, A Reynolds-Averaged Navier-Stokes Solver Using Unstructured Mesh-Based Finite-Volume Scheme, AIAA 98-0231- The gradients used in the diffusion term in Eq. 7 are computed by applying the divergence theorem with the average of reconstructed face values. - Mathur and Murthy, All Speed Flows on Unstructured Meshes Using a Pressure Correction Approach, AIAA 99-3365 - When evaluating diffusive fluxes the gradient  at each face is computed by first considering an average gradient at each face is computed by first considering an average gradient  composed of gradients within the two cells on either side of the face composed of gradients within the two cells on either side of the face  where the cell gradients where the cell gradients  and and  are evaluated using the divergence theorem (see Eq. 8), but are different from the reconstruction gradients appearing in Eq. 7 in that they are computed using an average of the reconstructed values are evaluated using the divergence theorem (see Eq. 8), but are different from the reconstruction gradients appearing in Eq. 7 in that they are computed using an average of the reconstructed values  and and  (as opposed to cell-average values), and are not limited. - Weiss, Maruszewski and Smith, Implicit Solution of the Navier-Stokes Equations on Unstructured Meshes, AIAA 97-2103 (as opposed to cell-average values), and are not limited. - Weiss, Maruszewski and Smith, Implicit Solution of the Navier-Stokes Equations on Unstructured Meshes, AIAA 97-2103- The same authors of the last sentence use it also in AIAA J. Vol. 37, N. 1, 1999: Implicit Solution of Preconditioned Navier-Stokes Equations Using Algebraic Multigrid. In contrast, the only paper where I found an explicit statement that a simple average of unlimited gradients on left and right is used for the cross diffusion is: A Multi-Dimensional Linear Reconstruction Scheme for Arbitrary Unstructured grids - Kim, Makarov and Caraeni, AIAA 2003-3990. Now, to me, there seems that, at least at some point back in the 90's, someone in Fluent was quite sure about this. I still have to try this, and I don't expect great differences (nor convenience in terms of computational costs), but it has a certain consistency. The whole algorithm now requires only face values: those for convection and those in the green gauss procedure for the cross diffusion gradients; both are computed via reconstruction gradients, which are the limited version of the base ones (which in contrast are not anymore needed). @Arjun: in case, following the reasoning above, I would use reconstruction gradients for face values (where possible and meaningful). For the armonic mean, do you use interpolation just along the normal to the face? However, I'm not exactly using the formulation I presented above, but a slight variant from the group of Straatman. As an alternative to the use of Hessians, it has an additional term that corrects the simple average of gradients in the cross diffusion term. But I never tried any comparison to see if it actually performs better than the pure average. |
|
|
|

|
|
|
|
|
#13 | |
|
Senior Member
|
Quote:
EDIT: While the work above is actually for unstructured grids, it also uses the simple average as per relation 2 in the first post above. Last edited by sbaffini; October 10, 2017 at 11:32. |
||
|
|

|
||
|
|
|
#14 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Paolo when you write
Int[a,b] f(x) dx = f_av * |b-a| f being in our case gamma*df/dn, the above relation is exact. Now you want to approximate f_av on the grid and that decide the accuracy order of the integration. Central point or trapezoidal rule is second order, only using Simpson you have higher order. Then I dont understand in case of second order PDE how you can have a mathematical discontinuity that does not allow to write the gradient |
|
|
|

|
|
|
|
|
#15 |
|
Senior Member
|
Yes, the point is: how to determine the value of the diffusion coefficient (I know how to do that for the derivative) in the central point, when such coefficient is variable in space? What is the minimum accuracy I need? The formulas I used above all seem to be only first order... is that enough? I don't think so...
Well, maybe the math may be correct but, if you have severe jumps of properties across a cell face, the fields on the two sides of such face might have severe jumps that, discretely, appear as discontinuities. The same happens for shock waves. The point is that evaluating the gradient across such discrete discontinuities is probably not accurate in any case. |
|
|
|

|
|
|
|
|
#16 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
But that has nothing to do with the type of grid (structured or unstructured) and the reconstruction of the gradient but only on the fact that high gradients, such as viscous shock layer (immagine somehow of the order 10^-6 - 10^-7 m), can not be represented on a practical grid. Howevere, as the diffusion term involves the difference of gradients, you have that is proportional to second derivatives that smooth the gradient. In other words, the problem is that the flow appears like it were inviscid for a viscous shock layer. And the key of the issue is in the reconstruction of the convective terms, not in the diffusive term. Do not forget that a code using a Riemann solver, use the face as a discontinuity surface between two different states. In a splitting method you can then solve for the diffusion on the smoothed variables. I immagine that your goal is to code a general gradient reconstruction for "all-velocity" flows, going from low Mach to high Mach number and considering the chance to implement an LES model. 
|
||
|
|

|
||
|
|
|
#17 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
A linear reconstruction for the diffusion coefficient is sufficient for a second order discretization. And do not forget that for the SGS viscosity you recontruct a function from discrete values that are affected by several model apporximations.. |
||
|
|

|
||
|
|
|
#18 | |
|
Senior Member
|
Quote:
Octree grid. Left cell is a cube of side 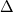 with center in with center in  . On the right (positive x), this cell has 4 neighbor cells, which are 1/8 of the volume of the left cell. Consider, for example, the one with all positive coordinates. This cell, our right cell, is a cube of side . On the right (positive x), this cell has 4 neighbor cells, which are 1/8 of the volume of the left cell. Consider, for example, the one with all positive coordinates. This cell, our right cell, is a cube of side  and center in and center in  . The centroid of the face shared by the left and right cells is, in this case, at . The centroid of the face shared by the left and right cells is, in this case, at  . .Question: given  in in  and and  in in  , how do I compute , how do I compute  in in  ? Note that the line connecting ? Note that the line connecting  and and  does not intersect the face in does not intersect the face in  . .Do I interpolate using only the  coordinate (the one normal to the face)? Or maybe it's fine using one of the methods I described above? coordinate (the one normal to the face)? Or maybe it's fine using one of the methods I described above?In any case, unless I use gradients of  , it seems to me that I can't achieve 2nd order accuracy for the value , it seems to me that I can't achieve 2nd order accuracy for the value  . However, I don't have gradients for . However, I don't have gradients for  in most cases, and I don't want to have them. It's just to know what options I really have. Also, non limited gradients would be too risky here. I need to be sure that in most cases, and I don't want to have them. It's just to know what options I really have. Also, non limited gradients would be too risky here. I need to be sure that  . .
|
||
|
|

|
||
|
|
|
#19 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Just to be clear, the linear approximate of the diffused field variable is only valid when the diffusivity is the neighboring cells are all the same, or at least the same order of magnitude. If you analyze the flux and force the value of the field and the diffusive flux at the faces to match, you get a set of relations that you can solve for the diffusive flux. On evenly spaced grids that are orthogonal (the line connecting the two cell centroids is parallel to the face normal), this reduces to harmonic averaging. There are distance terms that can account for the case of non-evenly spaced grids that are still orthogonal. The problems really arise when you have non-orthogonality. The flux balance conditions at the faces no longer reduce to two-equation sets that are trivially solvable. Again, you can make approximations that have error terms that are a function of non-orthonality and those work 99% of the time, but a skewed cell on a material boundary can make those break down, in my experience.
It is really a mess. Just recalling it is giving me PTSD. 8) |
|
|
|

|
|
|
|
|
#20 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
Quote:
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Discretization of the convective term of the N-S equation | Donton | Main CFD Forum | 1 | September 1, 2017 13:01 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| FVM discretization of diffusion term on crvlnr gr | Michail | Main CFD Forum | 3 | March 14, 2008 07:52 |
| TVD/NVD in unstructured grids | m.s. darwish | Main CFD Forum | 0 | August 24, 1999 14:44 |