 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
Member
Marco Ghiani
Join Date: Jan 2011
Posts: 35
Rep Power: 15  |
Hi everybody ! I'm trying to understand the implicit algorithm used here http://hmf.enseeiht.fr/travaux/CD000.../reportbid.htm , In Particolar what's the physicals meaning of the coefficient LAMBDA and ALPHA ?? in the calculation of the d array ? a sort of solution relazation or what ever ?
which range of values should have ? thanks in advance |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
If you work only with the convective and diffusive terms, then alpha=lambda=0 |
||
|
|

|
||
|
|
|
#3 |
|
Member
Marco Ghiani
Join Date: Jan 2011
Posts: 35
Rep Power: 15  |
Ok !! so I'm try to implement a implicit method (taking ideas from this implicit resolution .. ) but using matrices .. in this way I can taking account of the time marcing and obtain a matrix containg all the solution !
unfortunally I'm made a mistake .. I cannot find where ! could some body give a look to my simple code ?? Code:
MODULE PARAM
IMPLICIT NONE
INTEGER , PARAMETER :: DP = KIND(1.d0)
INTEGER , PARAMETER :: SP = KIND(1.0)
END MODULE
MODULE BURGER_2I
USE PARAM
IMPLICIT NONE
!-------------------
REAL(DP), PARAMETER :: x0 =0.D0,xF =1.D0,t0=0.D0,tF=1.D0
REAL(DP), PARAMETER :: dx = 0.005!0.005
REAL(DP), PARAMETER :: dt = 0.01!0.01
REAL(DP), PARAMETER :: nu = 10E-3
INTEGER , PARAMETER :: N = CEILING((XF-X0)/DX)
INTEGER , PARAMETER :: M = CEILING((tF-t0)/DT)
REAL(DP), DIMENSION(N+1,M+1) :: a, b, c, d , c2, d2
REAL(DP), PARAMETER :: R= nu*dt/dx**2 , K= dt/(2*dx)
REAL(DP), PARAMETER :: LAMBDA= 0.d0 , ALPHA= 0.d0
INTEGER , PARAMETER :: cl = 1
REAL(DP), PARAMETER :: pi = 3.14159265358979323846
REAL(DP), DIMENSION(N+1) :: aa, bb, cc, dd , cc2, dd2, u1
CONTAINS
!------------------------------------------------------------------------
SUBROUTINE BURGER_IMPLICIT (x,t,u)
USE PARAM
IMPLICIT NONE
REAL(DP) , DIMENSION(N+1) :: x ,u1
REAL(DP) , DIMENSION(M+1) :: t
REAL(DP) :: tt
REAL(DP) , DIMENSION(N+1,M+1) :: u
INTEGER :: i,j, stat
INTEGER :: tM
a = 0.d0
b = 0.d0
c = 0.d0
d = 0.d0
x(1:N+1) = (/( (x0 + dx*(i-1)), i=1,N+1) /)
t(1:M+1) = (/( (t0 + dt*(j-1)), j=1,M+1) /)
U(1:N+1,1:M+1) = RESHAPE((/ ((( sin(2*pi*(i-1))/N ), i=1,N+1),j=1,M+1) /),(/N+1,M+1/))
!------------------- Inizializing using IMPLICIT-DO loop
a(2:N+1,1:M+1) = RESHAPE((/ (((-0.25*dt/dx*U(i-1,j)), i=2,N+1),j=1,M+1) /),(/N,M+1/))
b(1:N+1,1:M+1) = 1 + R
c(1:N ,1:M+1) = RESHAPE((/ ((( 0.25*dt/dx*U(i+1,j)), i=1,N) ,j=1,M+1) /),(/N,M+1/))
d(1,1:M+1) = (/((1-R)*U(1,j) + 0.5*R*U(2,j), j=1,M+1)/)
d(N+1,1:M+1) = (/( 0.5*R*u(N,j) + (1-R)* u(N+1,j), j=1,M+1 )/)
d(2:N,1:M+1) = RESHAPE((/ (((0.5*R*u(i-1,j)+ &
& (1-R)*u(i,j)*0.5*R*u(i+1,j)+dt*(LAMBDA*u(i,j)+ALPHA*u(i,j)**3)) ,i=2,N),j=1,M+1)/),(/N-1,M+1/))
! DO j=1,M+1
! DO i=2,N
! d(i,j) = 0.5*R*u(i-1,j)+(1-R)*u(i,j)*0.5*R*u(i+1,j)+dt*(LAMBDA*u(i,j)+ALPHA*u(i,j)**3)
! END DO
! END DO
!-----------------------------------------------------------------------
!----------- THOMAS ALGORITHM
!-----------------------------------------------------------------------
c2(1,1:M+1) = (/ (c(1,j)/b(1,j), j=1,M+1) /)
d2(1,1:M+1) = (/ (d(1,j)/b(1,j), j=1,M+1) /)
c2(2:N+1,1:M+1) = RESHAPE((/(( c(i,j)/(b(i,j)-a(i,j)*c2(i-1,j)) , i=2,N+1), j=1,M+1)/),(/N,M+1/))
d2(2:N+1,1:M+1) = RESHAPE((/(( (d(i,j)-a(i,j)*d2(i-1,j))/(b(i,j)-a(i,j)*c2(i-1,j)),i=2,N+1) , &
& j=1,M+1)/),(/N,M+1/))
!-----------------------------------------------------------------------
!------------ BACKWARD BIDIAGONAL SISTEM RESOLUTION ~ ~
u(n+1,1:M+1) = dd2(n+1)
!Print*, shape(U) , shape(d2)
!U(1:N+1,1:M+1) = (/( )/)
DO j=1,M+1
DO i=1,N
u(N+1-i , j) = d2(N+1-i,j) - u(N-i+2,j) * c2(n+1-i,j)
END DO
END DO
OPEN(UNIT=10,FILE='implicit_burger.dat',STATUS='UNKNOWN',IOSTAT=stat)
IF (stat .NE. 0) THEN
WRITE(6,'(A)') 'Error opening file ''implicit_burger.dat''!, EXIT 1'
STOP
ELSE
DO j=1,M+1
WRITE (10,FMT='(3E20.8)') (x(i) , t(j) , u(i,j), i=1,N+1)
WRITE (10,*)
! WRITE (6,FMT='(50("-"))')
END DO
END IF
CLOSE(10)
OPEN(20,file='i_burger.dat',STATUS='UNKNOWN',IOSTAT=stat)
IF (STAT .NE. 0) THEN
WRITE(6,FMT='(A)')'Error opening File ''bur1.dat'' (EXIT1)'
STOP
ELSE
!DO j=1,M+1
!WRITE(10,FMT='(3F20.5)') (x(i), t(j) ,u(i,j), i=1,N+1) !((u(i,j) , i=1,N+1), J=1,M+1)
WRITE(20,*)
WRITE(20,FMT='(2E20.8)') (x(i), u1(i), i=1,N) !((u(i,j) , i=1,N+1), J=1,M+1)
!WRITE(6,'(50("-"))')
!END DO
END IF
CLOSE(20)
RETURN
END SUBROUTINE
!------------------------------------------------------------------------
END MODULE
Code:
PROGRAM main
USE BURGER_2I
IMPLICIT NONE
REAL(DP) , DIMENSION (N+1) :: xx
REAL(DP) , DIMENSION (M+1) :: tt
REAL(DP) , DIMENSION (n+1,M+1) :: UU
CALL BURGER_IMPLICIT(xx,tt,UU)
!CALL
STOP
END
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
What error do you get?
|
|
|
|

|
|
|
|
|
#5 |
|
Member
Marco Ghiani
Join Date: Jan 2011
Posts: 35
Rep Power: 15  |
the compilation and link goes always successfully , but the result are surreal, you can try the code for better understanding
! |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
At present I cannot compile it, "surreal" means nothing to understand the issue. Are you encountering a numerical instability? Have you first completed the code for the simple FTUS scheme on periodic condition? That is the first step to check first the code structure and then implement other schemes |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Just an observation: I would not use Crank-Nicholson for the burgers equation unless you perform some operator splitting, i.e. Lax-Freidrichs for the nonlinear advective term and Crank-Nicholson for the diffusion term.
EDIT: Your solution would be more stable with a scheme such as MacCormack than doing pure implicit integration. |
|
|
|

|
|
|
|
|
#8 | |
|
Member
Marco Ghiani
Join Date: Jan 2011
Posts: 35
Rep Power: 15  |
Quote:

|
||
|
|

|
||
|
|
|
#9 | |
|
Member
Marco Ghiani
Join Date: Jan 2011
Posts: 35
Rep Power: 15  |
Quote:
|
||
|
|

|
||
|
|
|
#10 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
||
|
|

|
|
|
|
|
#11 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
Hi,
Given you are working with the viscous Burgers equation your scheme will look like this: First we solve for the advection term: 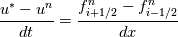 where 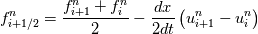 Secondly, we solve for the viscous term: 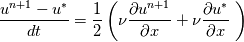 You will get a tridiagonal matrix [1, -2, 1] If the operators do not commute you will have to perform either Strang splitting or alternate the splitting to get second order accuracy. |
|
|
|

|
|
|
|
|
#12 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
Actually, you do not need to perform a splitting, just discretize the convective and diffusive and solve 
|
|
|
|

|
|
|
|
|
#13 |
|
Senior Member
Selig
Join Date: Jul 2016
Posts: 213
Rep Power: 11  |
I agree with you. Is there a reason why people would rather not use operator splitting aside from the problem of non-commuting operators?
|
|
|
|

|
|
|
|
|
#14 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
Quote:
The problem is in the order of accuracy of the adopted splitting where some operators do not commute. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Guide: Writing Equations in LaTeX on the CFD Online Forums | pete | Site Help, Feedback & Discussions | 27 | May 19, 2022 04:19 |
| Implicit versus Explicit | Deepak | Main CFD Forum | 17 | November 7, 2015 14:14 |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 07:27 |
| CFD governing equations | m.gos | Main CFD Forum | 0 | April 30, 2011 15:21 |
| Implicit Euler equations | moein_joon27 | Main CFD Forum | 1 | January 13, 2011 15:43 |