Turbulent Jet

FMDenaro · October 13, 2017, 14:40

Quote:

Originally Posted by selig5576

Dr. Denaro,

I agree, however I believe I am already doing this when I solve the PPE at the boundary:

$R_{nx-1,j} = \frac{\rho}{dt} \left(\frac{u^{n+1}_{nx,j} - uf^{*}_{nx-2,j}}{dx} + \frac{vf^{*}_{2,j} - vf^{*}_{2,j-1}}{dy} \right)$

$P_{nx-1,j} = (1 - \omega) P_{nx-1,j} + \frac{\omega}{\frac{1}{dx^{2}} + \frac{2}{dy{2}}} \left(\frac{P_{nx-2,j}}{dx^{2}} + \frac{1}{dy^{2}} \left(P_{nx-1,j+1} + P_{nx-1,j-1}\right) - R_{nx-1,j}\right)$

In this case $u_{nx,j}^{n+1} = u_{nx-1,j}^{n+1}$ as I have an outflow BC. I could be wrong, but I do not set this in the PPE, but rather when I set the boundary conditions for $u^{n+1}, v^{n+1}$ .

Not sure about you index notation in the PPE but you should have a row of the pressure matrix modified congruently by the BC while, conversely, I see still 5 elements in the row instead of 4.
Then, while computing cont(i,j) have you already stored the physical values of the velocity in ufnew and vfnew at the boundaries?

selig5576 · October 13, 2017, 15:02

Dr. Denaro,

The way I am handling the boundary conditions for the PPE is as outlined in the image (I did not have room in the message box.) The only thing I am doing differently, is $uf^{n+1}_{1,j} = u^{n+1}_{1,j}$

FMDenaro · October 13, 2017, 15:08

Ok, that's correct, I was wrong in reading the equation

selig5576 · October 13, 2017, 16:29

Quote:

Originally Posted by FMDenaro

Not sure about you index notation in the PPE but you should have a row of the pressure matrix modified congruently by the BC while, conversely, I see still 5 elements in the row instead of 4.
Then, while computing cont(i,j) have you already stored the physical values of the velocity in ufnew and vfnew at the boundaries?

When calculating cont(i,j) I have it before I do the velocity update, i.e. u = un, v = vn since we don't know un and vn yet.

So with my current formulation, is my BC for my PPE correct? I.e., even for outflow BC is setting $uf^{*}_{nx,j} = uf^{n+1}_{nx,j}$ . It illudes me why my PPE won't converge due to a simple outflow BC...

FMDenaro · October 13, 2017, 17:40

Correct for Dirichlet bc.s on the velocity but how do you work for Neuman on the velocity??

selig5576 · October 14, 2017, 14:30

The way I am handling the outflow BC is as follows

Using $uf^{n+1}_{i,j}, vf^{n+1}_{i,j}$ as defined in the previous post, I am imposing

on the continuity equation that is formed from the $uf^{n+1}_{i,j}, vf^{n+1}_{i,j}$ veleocities which gives

$\frac{uf^{n+1}_{i,j} - uf^{n+1}_{i-1,j}}{dx} + \frac{vf^{n+1}_{i,j} - vf^{n+1}_{i,j-1}}{dy} = 0$

Since I am interested in imposing the Neumann BC at the outlet (i=nx) I get

$\frac{uf^{n+1}_{nx,j} - uf^{n+1}_{nx-1,j}}{dx} + \frac{vf^{n+1}_{nx,j} - vf^{n+1}_{nx,j-1}}{dy} = 0$

I am imposing that $uf^{n+1}_{nx,j} = u^{n+1}_{nx,j} = u^{n+1}_{OUT}$ which gives

$\frac{u^{n+1}_{nx,j} - uf^{n+1}_{nx-1,j}}{dx} + \frac{vf^{n+1}_{nx,j} - vf^{n+1}_{nx,j-1}}{dy} = 0$

Expanding the terms and using SOR at the boundary I get

$P_{nx-1,j} = (1 - \omega) P_{nx-1,j} +D \left(\frac{1}{dx^{2}} P_{nx-2,j} + \frac{1}{dy^{2}} \left(P_{nx-1,j+1} + P_{nx-1,j-1} \right) - R_{nx-1,j}\right)$
$D = \frac{\omega}{1/dx^{2} + 2/dy^{2}}$
$R_{nx-1,j} =\frac{\rho}{dt} \left(\frac{u^{n+1}_{nx,j} - uf^{n+1}_{nx-2,j}}{dx} + \frac{vf^{n+1}_{nx-1,j} - vf^{n+1}_{nx-1,j-1}}{dy} \right)$

Now, it is only after I calculate the un, vn (the corrector step), do I set $u^{n+1}_{nx,j} = u^{n+1}_{nx-1,j}$

Something else to mention, if I set P(2,2) = 1.0 and using un(nx,j) = un(nx-1,j), vn(nx,j) = vn(nx-1,j), while my solver doesnt crash (because I've created a fixed point), my jet doesnt ever really form. By that I mean the jet stops growing after 200 time steps. My theory is that since my pressure BCs are not correct, its affecting the jet formation.

To further isolate any bug, I have rewritten my solver in Matlab where I am using a basic explicit euler time integration.

Code:

close all;
clear all;
  
Lx = 1;               
Ly = 1;                
  
nx = 30;              
ny = 30;              
  
dx = Lx/(nx-1);        
dy = Ly/(ny-1);       
  
dt = 0.0001;          
  
rho = 1.0;  
nu =  0.1; 
                   
omega = 1.9;
  
IterMax = 15000;        
tol = 1e-6;
tEnd = 2.00;
  
x = zeros(nx,ny);               
y = zeros(nx,ny);
  
R =  zeros(nx,ny); 
P = zeros(nx,ny);
Res = zeros(nx,ny);
  
Cx = zeros(nx,ny);              
Cy = zeros(nx,ny);              
  
Dx = zeros(nx,ny);              
Dy = zeros(nx,ny);   
  
u = zeros(nx,ny);               
v = zeros(nx,ny);
  
us = zeros(nx,ny);
vs = zeros(nx,ny);
  
un = zeros(nx,ny);
vn = zeros(nx,ny);
  
uf = zeros(nx,ny);
vf = zeros(nx,ny);
  
ufs = zeros(nx,ny);
vfs = zeros(nx,ny);
  
Qx = zeros(nx,ny);
Qy = zeros(nx,ny);
  
DivU = zeros(nx,ny);

for j=1:ny
    for i=1:nx
        u(i,j) = 0.0;
        v(i,j) = 0.0;
        P(i,j) = 0.0;
    end 
end

for j=1:ny
    for i=1:nx
        x(i,j) = (i-1)*dx;
        y(i,j) = (j-1)*dy;
    end
end
  
t = 0.0;
  
while (t < tEnd)
    for j=1:ny
        for i=1:nx-1
            uf(i,j) = 0.5*(u(i+1,j) + u(i,j));
        end
    end
      
    for j=1:ny-1
        for i=1:nx
            vf(i,j) = 0.5*(v(i,j+1) + v(i,j));
        end
    end
    
    for j=2:ny-1
        for i=2:nx-1
            Dx(i,j) = nu*(1.0/dx^2*(u(i+1,j) - 2.0*u(i,j) + u(i-1,j)) + 1.0/dy^2*(u(i,j+1) - 2*u(i,j) + u(i,j-1)));                                   
            Dy(i,j) = nu*(1.0/dx^2*(v(i+1,j) - 2.0*v(i,j) + v(i-1,j)) + 1.0/dy^2*(v(i,j+1) - 2*v(i,j) + v(i,j-1)));  
              
            Cx(i,j) = (1.0/dx)*(uf(i,j).*uf(i,j) - uf(i-1,j).*uf(i-1,j)) + (1.0/dy)*(uf(i,j).*vf(i,j) - uf(i,j-1).*vf(i,j-1));
            Cy(i,j) = (1.0/dx)*(uf(i,j).*vf(i,j) - uf(i-1,j).*vf(i-1,j)) + (1.0/dy)*(vf(i,j).*vf(i,j) - vf(i,j-1).*vf(i,j-1));
              
            Qx(i,j) = -Cx(i,j) + Dx(i,j);
            Qy(i,j) = -Cy(i,j) + Dy(i,j);
              
            us(i,j) = u(i,j) + dt*Qx(i,j);
            vs(i,j) = v(i,j) + dt*Qy(i,j);
        end
    end
 
    
    us(1,:) = un(1,:);
    us(nx,:) = un(nx,:);
    us(:,1) = un(:,1);
    us(:,ny) = un(:,ny);
    
    vs(1,:) = vn(1,:);
    vs(nx,:) = vn(1,:);
    vs(:,1) = vn(:,1);
    vs(:,ny) = vn(:,ny);
      
    for j=1:ny
        for i=1:nx-1
            ufs(i,j) = 0.5*(us(i+1,j) + us(i,j));
        end
    end
      
    for j=1:ny-1
        for i=1:nx
            vfs(i,j) = 0.5*(vs(i,j+1) + vs(i,j));
        end
    end
      
    for j=3:ny-2
        for i=3:nx-2
            R(i,j) = (rho/dt)*((1/dx)*(ufs(i,j) - ufs(i-1,j)) + (1/dy)*(vfs(i,j) - vfs(i,j-1)));
        end
    end
    
    Iter = 0;
      
    while (Iter <= IterMax)              
        for j=3:ny-2
            for i=3:nx-2
                P(i,j) = (1-omega)*P(i,j) + omega/(2/dx^2 + 2/dy^2)*((P(i+1,j) + P(i-1,j))/dx^2 + (P(i,j+1) + P(i,j-1))/dy^2 - R(i,j));
            end
        end
          
        for j=3:ny-2
            R(2,j) = (rho/dt)*((1/dx)*(ufs(2,j) - un(1,j)) + (1/dy)*(vfs(2,j) - vfs(2,j-1)));
            P(2,j) = (1-omega)*P(2,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(3,j) + (1/dy^2)*(P(2,j+1) + P(2,j-1)) - R(2,j));
      
            %Outflow BC, point of interest
            R(nx-1,j) = (rho/dt)*((1.0/dx)*(un(nx-1,j) - ufs(nx-2,j)) + (1/dy)*(vfs(nx-1,j) - vfs(nx-1,j-1)));
            P(nx-1,j) = (1-omega)*P(nx-1,j) + omega/(1/dx^2 + 2/dy^2)*((1/dx^2)*P(nx-2,j) + (1/dy^2)*(P(nx-1,j+1) + P(nx-1,j-1)) - R(nx-1,j));
        end
  
        for i=3:nx-2
            R(i,2) = (rho/dt)*((1/dx)*(ufs(i,2) - ufs(i-1,2)) + (1/dy)*(vfs(i,2) - vn(i,1)));
            P(i,2) = (1-omega)*P(i,2) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,2) + P(i-1,2)) + (1/dy^2)*P(i,3) - R(i,2));
     
            R(i,ny-1) = (rho/dt)*((1/dx)*(ufs(i,ny-1) - ufs(i-1,ny-1)) + (1/dy)*(vn(i,ny) - vfs(i,ny-2)));
            P(i,ny-1) = (1-omega)*P(i,ny-1) + omega/(2/dx^2 + 1/dy^2)*((1/dx^2)*(P(i+1,ny-1) + P(i-1,ny-1)) + (1/dy^2)*P(i,ny-2) - R(i,ny-1));
        end
          
        R(2,ny-1) = (rho/dt)*((1/dx)*(ufs(2,ny-1) - un(1,ny-1)) + (1/dy)*(v(2,ny) - vfs(2,ny-1)));
        P(2,ny-1) = (1-omega)*P(2,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(3,ny-1) + (1/dy^2)*P(2,ny-2) - R(2,ny-1));
            
      
        R(nx-1,2) = (rho/dt)*((1/dx)*(un(nx,2) - ufs(nx-2,2)) + (1/dy)*(vfs(nx-1,2) - vn(nx-1,1)));
        P(nx-1,2) = (1-omega)*P(nx-1,2) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,2) + (1/dy^2)*P(nx-1,3) - R(nx-1,2));
            
        R(nx-1,ny-1) = (rho/dt)*((1/dx)*(un(nx,ny-1) - ufs(nx-2,ny-1)) + (1/dy)*(vn(nx-1,ny) - vfs(nx-1,ny-2)));
        P(nx-1,ny-1) = (1-omega)*P(nx-1,ny-1) + omega/(1/dx^2 + 1/dy^2)*((1/dx^2)*P(nx-2,ny-1) + (1/dy^2)*P(nx-1,ny-2) - R(nx-1,ny-1));
         
        %R(2,2) = (rho/dt)*((1.0/dx)*(ufs(2,2) - un(1,2)) + (1.0/dy)*(vfs(2,2) - vn(2,1)));
        %P(2,2) = (1-omega)*P(2,2) + omega/(1.0/dx^2 + 1.0/dy^2)*((1.0/dx^2)*P(3,2) + (1.0/dy^2)*P(2,3) - R(2,2));
       P(2,2) = 1.0;
        Res = 0.0;
         
        for j=3:ny-2
            for i=3:nx-2
                Res(i,j) = ((1.0/dx^2)*(P(i-1,j) - 2*P(i,j) + P(i+1,j)) + (1.0/dy^2)*(P(i,j-1) - 2*P(i,j) + P(i,j+1))) - R(i,j);
            end
        end
          
        error = sqrt(dx*dy*sum(sum(Res.^2)));
          
        if (error >= tol)
            Iter = Iter + 1;
        else
            fprintf("PPE has Converged")
            break;
        end
    end 
     
    P(1,:) = P(2,:) + (dx/dt)*(us(1,:) - un(1,:));
    P(nx,:) = P(nx-1,:) - (dx/dt)*(us(nx,:) - un(nx,:));
    P(:,1) = P(:,2) + (dy/dt)*(vs(:,1) - vn(:,1));
    P(:,ny) = P(:,ny-1) - (dy/dt)*(vs(:,ny) - vn(:,ny));
   
    for j=2:ny-1
        for i=2:nx-1
            un(i,j) = us(i,j) - (dt/(2.0*dx*rho))*(P(i+1,j) - P(i-1,j));
            vn(i,j) = vs(i,j) - (dt/(2.0*dy*rho))*(P(i,j+1) - P(i,j-1));
        end
    end
  
    un(:,ny) = 0.0;
    %basic inlet profile
    un(1,12:15) = 1.0;
    %outflow BC for u
    un(nx,:) = u(nx-1,j);
    un(:,1) = 0.0;
  
    %Set outflow BC for v
    vn(nx,:) = v(nx-1,j);
    vn(1,:) = 0.0; 
    vn(:,ny) = 0.0; 
    vn(:,1) = 0.0; 
      
    u = un;
    v = vn;
      
   
    t = t + dt
      
    contourf(x,y,un,20);
    colormap jet
    xlabel('x');
    ylabel('y');
    title(['t = ',num2str(t)]);
    pause(0.001);
end

FMDenaro · October 14, 2017, 14:43

"I am imposing that

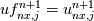which gives"

This way I don't see any Neumann BC.s ... you should start from the relation

u*=u^n+1+ dP/dx - > du*/dx=d^n+1/dx+d2P/dx2 -> du*/dx=d2P/dx2

selig5576 · October 15, 2017, 12:59

Given the relation you provided, I have tried to formulate a BC, and this is what I have.

I consider

$\frac{P_{i-1,j} - 2P_{i,j} + P_{i+1,j}}{dx^{2}} + \frac{P_{i,j-1} - 2P_{i,j} + P_{i,j+1}}{dy^{2}} = R_{i,j}$
$R_{i,j } = \frac{\rho}{dt} \left(\frac{uf^{*}_{i,j} - uf^{*}_{i-1,j}}{dx} + \frac{vf^{*}_{i,j} - vf^{*}_{i,j-1}}{dy} \right)$
Using the relation $\frac{\partial^{2} P}{\partial x^{2}} = \frac{uf^{*}_{i,j} - uf^{*}_{i-1,j}}{dx}$ and evaluating at the outflow I get

$\frac{P_{i,j-1} - 2P_{i,j} + P_{i,j+1}}{dy^{2}} = \frac{\rho}{dt} \left(\frac{vf^{*}_{i,j} - vf^{*}_{i,j-1}}{dy} \right)$

Using SOR and evaluating at the boundary I get

$P_{i,j} = (1 - \omega)P_{i,j} + \frac{\omega}{2 dy^{2}} \left(\frac{P_{i,j-1} + P_{i,j+1}}{dy^{2}} - \frac{vf^{*}_{i,j} - vf^{*}_{i,j-1}}{dy} \right)$

I then evaluate at i=nx-1. Is there literature on outflow BC for PPEs on colocated grids? I was unable to find anything...

FMDenaro · October 15, 2017, 13:47

Well, we need to be careful in the index and colocation. I assume (I hope to be right) that i=nx is the index for the faces outflow. The equation for the pressure is written in the interior node shifted from the outflow face by -dx/2, right?

Therefore, the Neumann BC.s is fromally written on the faces outflow then you insert them in the PPE. However, I see that one can work in different ways. I believe that a simple way is to write the BC directly at the node of the PPE, this way you have a tridiagonal system along y

selig5576 · October 15, 2017, 14:10

Quote:

The equation for the pressure is written in the interior node shifted from the outflow face by -dx/2, right?

That is correct, hence my indexing for the interior is i=3,nx-2 and j=3,ny-2. With $\frac{\partial^{2} P}{\partial x^{2}} = \frac{\partial u^{*}}{\partial x}$ , I do get a tridiagonal matrix along y. By PPE node do you mean at i=nx? If it is not too trouble, an example would be quite helpful

FMDenaro · October 15, 2017, 14:17

Quote:

Originally Posted by selig5576

That is correct, hence my indexing for the interior is i=3,nx-2 and j=3,ny-2. With $\frac{\partial^{2} P}{\partial x^{2}} = \frac{\partial u^{*}}{\partial x}$ , I do get a tridiagonal matrix along y. By PPE node do you mean at i=nx? If it is not too trouble, an example would be quite helpful

Maybe the pressure equation written at i=nx-1, isnt'it?
To tell the truth, at present I don't remember a textbook where you can find an example for the implementation of outflow BC.s in the pressure equation on colocated grid.

selig5576 · October 15, 2017, 14:36

No problem. My mistake, it should be i=nx-1.

Quote:

"I am imposing that which gives"

This way I don't see any Neumann BC.s ... you should start from the relation

u*=u^n+1+ dP/dx - > du*/dx=d^n+1/dx+d2P/dx2 -> du*/dx=d2P/dx2

So I should evaluate the PPE at i=nx-1

$\frac{P_{nx-2,j} - 2P_{nx-1,j} + P_{nx,j}}{dx^{2}} + \frac{P_{nx-1,j-1} - 2P_{nx-1,j} + P_{nx-1,j+1}}{dy^{2}} =R_{nx-1,j}$

$R_{nx-1,j} = \frac{\rho}{dt} \left(\frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx} + \frac{vf^{*}_{nx-1,j} - vf^{*}_{nx-1,j-1}}{dy} \right)$

Now since I am evaluating the PPE at the boundary I then insert

$\frac{P_{nx-2,j} - 2P_{nx-1,j} + P_{nx,j}}{dx^{2}} = \frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx}$

Solving for $P_{nx,j}$ I get

$P_{nx,j} =- P_{nx-2,j} - 2P_{nx-1,j} + dx^{2} \frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx}$

And this goes into the PPE evaluated at i=nx-1? I feel like this is not right. Pardon the foolishness.

FMDenaro · October 15, 2017, 15:03

Quote:

Originally Posted by selig5576

No problem. My mistake, it should be i=nx-1.

So I should evaluate the PPE at i=nx-1

$\frac{P_{nx-2,j} - 2P_{nx-1,j} + P_{nx,j}}{dx^{2}} + \frac{P_{nx-1,j-1} - 2P_{nx-1,j} + P_{nx-1,j+1}}{dy^{2}} =R_{nx-1,j}$

$R_{nx-1,j} = \frac{\rho}{dt} \left(\frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx} + \frac{vf^{*}_{nx-1,j} - vf^{*}_{nx-1,j-1}}{dy} \right)$

Now since I am evaluating the PPE at the boundary I then insert

$\frac{P_{nx-2,j} - 2P_{nx-1,j} + P_{nx,j}}{dx^{2}} = \frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx}$

Solving for $P_{nx,j}$ I get

$P_{nx,j} =- P_{nx-2,j} - 2P_{nx-1,j} + dx^{2} \frac{uf_{nx-1,j}^{*} - uf_{nx-2,j}^{*}}{dx}$

And this goes into the PPE evaluated at i=nx-1? I feel like this is not right. Pardon the foolishness.

First, be careful to the ratio rho/dt you missed. Then, you can totally disregard the term in x and solving only the Pyy=(rho/dt) d(v*)/dy at i=nx-1. This way, you do not need to discretize the Neumann BC.

selig5576 · October 15, 2017, 17:24

Thanks for pointing that out, so here is what I have formulated (I think I was on the right track)

$\frac{P_{nx-1,j-1} - 2P_{nx-1,j} + P_{nx-1,j+1}}{dy^{2}} = \frac{\rho}{dt} \left(\frac{vf^{*}_{nx-1,j} - vf^{*}_{nx-1,j-1}}{dy} \right)$
Using SOR at the boundary we get
$P_{nx-1,j} = (1 - \omega) P_{nx-1,j} + \frac{\omega}{\frac{1}{dy^{2}} }\left(\frac{1}{dy^{2}} P_{nx-1,j-1} + P_{nx-1,j+1} - R_{nx-1,j}\right)$
$R_{nx-1,j} = \frac{\rho}{dt} \left(\frac{vf^{*}_{nx-1,j} - vf^{*}_{nx-1,j-1}}{dy} \right)$

This is using the relation $\frac{\partial^{2} P}{\partial x^{2}} = \frac{\rho}{dt} \frac{\partial u^{*}}{\partial x}$

FMDenaro · October 15, 2017, 17:32

Seems ok. Do not forget that you have in the corners to add the BC.s also for v^n+1. Generally the cycles of the SOR are programmed differently, out of the do cycles.

October 15, 2017, 12:59	outflow BC for PPE	#48
selig5576 Senior Member Selig Join Date: Jul 2016 Posts: 213 Rep Power: 11	Given the relation you provided, I have tried to formulate a BC, and this is what I have. I consider $\frac{P_{i-1,j} - 2P_{i,j} + P_{i+1,j}}{dx^{2}} + \frac{P_{i,j-1} - 2P_{i,j} + P_{i,j+1}}{dy^{2}} = R_{i,j}$ $R_{i,j } = \frac{\rho}{dt} \left(\frac{uf^{}_{i,j} - uf^{}_{i-1,j}}{dx} + \frac{vf^{}_{i,j} - vf^{}_{i,j-1}}{dy} \right)$ Using the relation $\frac{\partial^{2} P}{\partial x^{2}} = \frac{uf^{}_{i,j} - uf^{}_{i-1,j}}{dx}$ and evaluating at the outflow I get $\frac{P_{i,j-1} - 2P_{i,j} + P_{i,j+1}}{dy^{2}} = \frac{\rho}{dt} \left(\frac{vf^{}_{i,j} - vf^{}_{i,j-1}}{dy} \right)$ Using SOR and evaluating at the boundary I get $P_{i,j} = (1 - \omega)P_{i,j} + \frac{\omega}{2 dy^{2}} \left(\frac{P_{i,j-1} + P_{i,j+1}}{dy^{2}} - \frac{vf^{}_{i,j} - vf^{}_{i,j-1}}{dy} \right)$ I then evaluate at i=nx-1. Is there literature on outflow BC for PPEs on colocated grids? I was unable to find anything...

October 15, 2017, 17:24	Boundary condition	#54
selig5576 Senior Member Selig Join Date: Jul 2016 Posts: 213 Rep Power: 11	Thanks for pointing that out, so here is what I have formulated (I think I was on the right track) $\frac{P_{nx-1,j-1} - 2P_{nx-1,j} + P_{nx-1,j+1}}{dy^{2}} = \frac{\rho}{dt} \left(\frac{vf^{}_{nx-1,j} - vf^{}_{nx-1,j-1}}{dy} \right)$ Using SOR at the boundary we get $P_{nx-1,j} = (1 - \omega) P_{nx-1,j} + \frac{\omega}{\frac{1}{dy^{2}} }\left(\frac{1}{dy^{2}} P_{nx-1,j-1} + P_{nx-1,j+1} - R_{nx-1,j}\right)$ $R_{nx-1,j} = \frac{\rho}{dt} \left(\frac{vf^{}_{nx-1,j} - vf^{}_{nx-1,j-1}}{dy} \right)$ This is using the relation $\frac{\partial^{2} P}{\partial x^{2}} = \frac{\rho}{dt} \frac{\partial u^{*}}{\partial x}$

Similar Threads
Thread	Thread Starter	Forum	Replies	Last Post
Problem with divergence	TDK	FLUENT	13	December 14, 2018 07:00
LES of Turbulent Jet	knuckles	OpenFOAM Running, Solving & CFD	1	March 31, 2016 20:33
turbulent jet	ramo	Main CFD Forum	1	September 4, 2005 08:43
Modelling a turbulent jet and k-epsilon constants	Ant	Siemens	3	January 24, 2005 16:56
Turbulent Intensity good or bad for a jet	Christian	Main CFD Forum	0	November 19, 2003 06:47

October 13, 2017, 15:08		#43
FMDenaro Senior Member Filippo Maria Denaro Join Date: Jul 2010 Posts: 6,849 Rep Power: 73	Ok, that's correct, I was wrong in reading the equation

October 13, 2017, 17:40		#45
FMDenaro Senior Member Filippo Maria Denaro Join Date: Jul 2010 Posts: 6,849 Rep Power: 73	Correct for Dirichlet bc.s on the velocity but how do you work for Neuman on the velocity??

October 14, 2017, 14:43		#47
FMDenaro Senior Member Filippo Maria Denaro Join Date: Jul 2010 Posts: 6,849 Rep Power: 73	"I am imposing that which gives" This way I don't see any Neumann BC.s ... you should start from the relation u=u^n+1+ dP/dx - > du/dx=d^n+1/dx+d2P/dx2 -> du*/dx=d2P/dx2

October 15, 2017, 13:47		#49
FMDenaro Senior Member Filippo Maria Denaro Join Date: Jul 2010 Posts: 6,849 Rep Power: 73	Well, we need to be careful in the index and colocation. I assume (I hope to be right) that i=nx is the index for the faces outflow. The equation for the pressure is written in the interior node shifted from the outflow face by -dx/2, right? Therefore, the Neumann BC.s is fromally written on the faces outflow then you insert them in the PPE. However, I see that one can work in different ways. I believe that a simple way is to write the BC directly at the node of the PPE, this way you have a tridiagonal system along y

October 15, 2017, 17:32		#55
FMDenaro Senior Member Filippo Maria Denaro Join Date: Jul 2010 Posts: 6,849 Rep Power: 73	Seems ok. Do not forget that you have in the corners to add the BC.s also for v^n+1. Generally the cycles of the SOR are programmed differently, out of the do cycles.