[FMDenaro]

That is the profile at the inlet?? First, the magnitude order is 10^-8, then it has positive and negative values...something is wrong

[selig5576]

I agree with you. I get larger values if I have my pressure initial condition to be 1.0. I am thinking there is a bug in my solver and its not my inlet.

[selig5576]

To better isolate the problem, I have gone back to my 2D incompressible code. To ensure my code is validated I tested it on the lid driven cavity and I get good results. I now am trying to setup a 2D planar jet.
What I have found is that when I setup the outflow boundary conditions, my solver crashes, i.e. I get NaNs.

It is interesting to note that I only crash when I have outflow BC (Neumann BC). If I set one of the corner pressure BCs to 1.0 then my solver does not crash, however my numerical solution runs into problems as the compatibility condition isnt fully satisfied.

I have attached a link to my source code. A second pair of eyes would be greatly appreciated as I am unsure what I am doing wrong.

Technical specs of the solver:

- Shu TVD RK3 for both advection and diffusion
- Collocated-grid solver with Rhie-Chow interpolation
- Cartesian grid
- boundary conditions for the intermediate velocity (predictor step) are from Kim and Moin
- No slip BC on all asides except the inlet and outlet

[FMDenaro]

I would work on these cases:

1) laminar Poiseuille solution: inlet parabolic profile, outlet Neumann.
2) analytical Taylor solution: periodic conditions

[selig5576]

Dr. Denaro,

With regards to the first benchmark,

my solver crashes unless I remove the null space of PPE solution, i.e. P(2,2) = 1.0. Given I am working with the BCs of Kim and Moin, is there any particular treatment for the outlet BC I am not taking into account?

With respect to the TG vortex benchmark, I have not tested my solver on that yet.

[FMDenaro]

If it crashes then there is an error in the bc.s that do not fulfill the compatibility condition...

[selig5576]

I am of the same opinion, however I am unsure how my boundary conditions in the corrector step would not be satisfying the compatibility condition. I am of the understanding that a first order approximation for the outflow conditions is not optimal, but it should still not cause numerical problems as such.

! Main time integration loop
call CartesianGrid(x,y,dx,dy)
  call InitialCondition(u,v,P)

  t = 0.0
  do while (t <= t_end)
    call Momentum(u, v, uMtm, vMtm)

    do j=2,ny-1
        do i=2,nx-1
            us1(i,j) = u(i,j) + dt*uMtm(i,j)
            vs1(i,j) = v(i,j) + dt*vMtm(i,j)
        end do
    end do

    call IntermediateBC(us1,vs1,un,vn,P)
    call Momentum(us1,vs1,uMtm1,vMtm1)

    do j=2,ny-1
        do i=2,nx-1
            us2(i,j) = (3.0/4.0)*u(i,j) + (1.0/4.0)*us1(i,j) + (dt/4.0)*uMtm1(i,j)
            vs2(i,j) = (3.0/4.0)*v(i,j) + (1.0/4.0)*vs1(i,j) + (dt/4.0)*vMtm1(i,j)
        end do
    end do

    call IntermediateBC(us2,vs2,un,vn,P)
    call Momentum(us2,vs2,uMtm2,vMtm2)

    do j=2,ny-1
        do i=2,nx-1
            us(i,j) = (1.0/3.0)*u(i,j) + (2.0/3.0)*us2(i,j) + ((2.0*dt)/3.0)*uMtm2(i,j)
            vs(i,j) = (1.0/3.0)*v(i,j) + (2.0/3.0)*vs2(i,j) + ((2.0*dt)/3.0)*vMtm2(i,j)
        end do
    end do

    call IntermediateBC(us,vs,un,vn,P)
    call PressureSolver(P,us,vs,un,vn)

    do j=2,ny-1
      do i=2,nx-1
        un(i,j) = us(i,j) - (dt/(2.0*dx*rho))*(P(i+1,j) - P(i-1,j))
        vn(i,j) = vs(i,j) - (dt/(2.0*dy*rho))*(P(i,j+1) - P(i,j-1))
      end do
    end do

   ! Set BCs for u^(n+1), v^(n+1)
    do i=1,nx
        un(i,1) = 0.0
        un(i,ny) = 0.0
        vn(i,1) = 0.0
        vn(i,ny) = 0.0
    end do

    do j=15,17
        un(1,j) = y(1,j)*(2.0 - y(1,j))
    end do

    do j=1,ny
        un(nx,j) = un(nx-1,j)
        vn(1,j) = 0.0
        vn(nx,j) = vn(nx-1,j)
    end do


    u = un
    v = vn

    t = t + dt

    print *, "t = ", t
  end do

! BCs
subroutine IntermediateBC (us, vs, un, vn, P)
        implicit none
        integer :: i, j
        double precision, dimension(nx,ny), intent(inout) :: un, vn, us, vs, P

        do j=1,ny
            us(1,j) = un(1,j) + (dt/dx)*(P(2,j) - P(1,j))
            us(nx,j) = un(nx,j) + (dt/dx)*(P(nx,j) - P(nx-1,j))

            vs(1,j) = vn(1,j) + (dt/dx)*(P(2,j) - P(1,j))
            vs(nx,j) = vn(nx,j) + (dt/dx)*(P(nx,j) - P(nx-1,j))
        end do

        do i=1,nx
            us(i,1) = un(i,1) + (dt/dy)*(P(i,2) - P(i,1))
            us(i,ny) = un(i,ny) + (dt/dy)*(P(i,ny) - P(i,ny-1))

            vs(i,1) = vn(i,1) + (dt/dy)*(P(i,2) - P(i,1))
            vs(i,ny) = vn(i,ny) + (dt/dy)*(P(i,ny) - P(i,ny-1))
        end do

        return
end subroutine IntermediateBC

!Momentum discretization for u, v

subroutine Momentum (u, v, uMtm, vMtm)
    implicit none
    integer :: i, j
    double precision, dimension(nx,ny), intent(out) :: uMtm, vMtm
    double precision, dimension(nx,ny), intent(inout) :: u, v
    double precision, dimension(nx,ny) :: Cx, Cy;
    double precision, dimension(nx,ny) :: Vx, Vy
    double precision, dimension(nx,ny) :: uf, vf

    call FaceVelocities(u,v,uf,vf)
    call BoundaryConditions(uf,vf)

    do j=2,ny-1
        do i=2,nx-1
            Cx(i,j) = (1.0/dx)*(uf(i,j)*uf(i,j) - uf(i-1,j)*uf(i-1,j)) + (1.0/dy)*(uf(i,j)*vf(i,j) - uf(i,j-1)*vf(i,j-1))
            Cy(i,j) = (1.0/dx)*(uf(i,j)*vf(i,j) - uf(i-1,j)*vf(i-1,j)) + (1.0/dy)*(vf(i,j)*vf(i,j) - vf(i,j-1)*vf(i,j-1))

            Vx(i,j) = nu*((1.0/dx**2)*(u(i-1,j) - 2.0*u(i,j) + u(i+1,j)) + (1.0/dy**2)*(u(i,j-1) - 2.0*u(i,j) + u(i,j+1)))
            Vy(i,j) = nu*((1.0/dx**2)*(v(i-1,j) - 2.0*v(i,j) + v(i+1,j)) + (1.0/dy**2)*(v(i,j-1) - 2.0*v(i,j) + v(i,j+1)))

            uMtm(i,j) = -Cx(i,j) + Vx(i,j)
            vMtm(i,j) = -Cy(i,j) + Vy(i,j)
        end do
    end do
    return
end subroutine

[FMDenaro]

I have not read the code, are you following exactly the same formulation proposed in the paper of Kim and Moin but applied on a non-steggered grid?

Can you run a case where the inflow profile is parabolic and you set the same profile at the outflow so that you set Dirichlet BC.s everywhere? I am curious to see if the code still crashes.
If it works without fixing a pressure value and the Poiseuille solution is obtained, then we can approach the problem of the Neumann BC at the outflow.

PS: of course, set a low Re number, for example 10.

[selig5576]

I am using the BC method of Kim and Moin on a collocated grid and with purely explicit time integration. Eventually I want to have implicit treatment of diffusion, but I want to work in a controlled environment to minimize error. Attached is a photo where at the outlet I assign the profile I used for the inlet.

I was curious if you had a chance to look at my code if you saw anything wrong. I've gone over the entire code (only 300 lines) and still don't see an error.

EDIT: Here is a plot of my inlet profile

EDIT 2: In terms of the type of projection method, I am using the pressure-free projection method like that of Kim and Moin..

[FMDenaro]

1) if you use a fully explicit method, the BC.s described in the paper by Kim and Moin for the intermediate velocity are not used at all in your code! You just need to set v^n+1 or dp/dn on the boundary
2) what about the plot? is still the inlet of the jet case?

[selig5576]

Dr. Denaro, thank you for pointing out my blunder!. Since I removed my implicit solver, I forgot that the intermediate BC has to be changed. I have now set u* and v* to be u^n+1 and v^n+1 on the boundary. I changed my outlet to be a standard outlet, un(nx,j) = un(nx-1,j), vn(nx,j) = vn(nx-1,j), and I still crash...

subroutine IntermediateBC (us, vs, un, vn, P)
        implicit none
        integer :: i, j
        double precision, dimension(nx,ny), intent(out) :: un, vn, us, vs, P

        do j=1,ny
            us(1,j) = un(1,j) 
            us(nx,j) = un(nx,j) 

            vs(1,j) = vn(1,j)
            vs(nx,j) = vn(nx,j)
        end do

        do i=1,nx
            us(i,1) = un(i,1) 
            us(i,ny) = un(i,ny) 

            vs(i,1) = vn(i,1) 
            vs(i,ny) = vn(i,ny) 
        end do

        return
end subroutine IntermediateBC

[FMDenaro]

Originally Posted by selig5576

Dr. Denaro, thank you for pointing out my blunder!. Since I removed my implicit solver, I forgot that the intermediate BC has to be changed. I have now set u* and v* to be u^n+1 and v^n+1 on the boundary. I changed my outlet to be a standard outlet, un(nx,j) = un(nx-1,j), vn(nx,j) = vn(nx-1,j), and I still crash...

subroutine IntermediateBC (us, vs, un, vn, P)
        implicit none
        integer :: i, j
        double precision, dimension(nx,ny), intent(out) :: un, vn, us, vs, P

        do j=1,ny
            us(1,j) = un(1,j) 
            us(nx,j) = un(nx,j) 

            vs(1,j) = vn(1,j)
            vs(nx,j) = vn(nx,j)
        end do

        do i=1,nx
            us(i,1) = un(i,1) 
            us(i,ny) = un(i,ny) 

            vs(i,1) = vn(i,1) 
            vs(i,ny) = vn(i,ny) 
        end do

        return
end subroutine IntermediateBC

That should not affect the Poisson solver... I strongly suggest to start debugging the code in a careful way:
1) setup the BC for the exact Poiseuille solution with Dirichlet inflow and outflow.
2) Start only the first time step and compute the intermediate velocity and the pressure field. Check if the Poisson solver converges.
3) Sum them and check the final divergence of the velocity

[selig5576]

Something I did not consider is, do I need to be setting boundary conditions for Vx ,Vy,Cx,Cy? (Vx is Viscous terms for u-mom and Cx is convection terms for u-mom?)

Example:

    Cx(i,j) = (1.0/dx)*(uf(i,j)*uf(i,j) - uf(i-1,j)*uf(i-1,j)) + (1.0/dy)*(uf(i,j)*vf(i,j) - uf(i,j-1)*vf(i,j-1))
            Cy(i,j) = (1.0/dx)*(uf(i,j)*vf(i,j) - uf(i-1,j)*vf(i-1,j)) + (1.0/dy)*(vf(i,j)*vf(i,j) - vf(i,j-1)*vf(i,j-1))

            Vx(i,j) = nu*((1.0/dx**2.0)*(u(i-1,j) - 2.0*u(i,j) + u(i+1,j)) + (1.0/dy**2.0)*(u(i,j-1) - 2.0*u(i,j) + u(i,j+1)))
            Vy(i,j) = nu*((1.0/dx**2.0)*(v(i-1,j) - 2.0*v(i,j) + v(i+1,j)) + (1.0/dy**2.0)*(v(i,j-1) - 2.0*v(i,j) + v(i,j+1)))

            uMtm(i,j) = -Cx(i,j) + Vx(i,j)
            vMtm(i,j) = -Cy(i,j) + Vy(i,j)

I am really unsure what could be going wrong as it seems that any type of neumann (outflow) BC will cause my solver to give me NaNs...

EDIT: I tried using standard explicit euler and I still get the same result. I was thinking my RK time stepping could have been creating an error..

[FMDenaro]

viscous and convective terms BC.s are a consequence of the BC.s prescribed for the velocity

[selig5576]

Thats what I thought, just wanted to double check on a numerical level. So the divergence of the velocity field is quite small, however when I sum it, it gets rather large...2.2 at t = 1.0. The L2 error of the PPE is 9.6818155843085360E-007.


I am determining continuity via

ufnew(i,j) = 0.5*(us(i+1,j) + us(i,j)) - (dt/rho)*(P(i+1,j) - P(i,j))
vfnew(i,j) = 0.5*(vs(i,j+1) + vs(i,j)) - (dt/rho)*(P(i,j+1) - P(i,j))

cont(i,j) = (1.0/dx)*(ufnew(i,j) - ufnew(i-1,j)) + (1.0/dy)*(vfnew(i,j) - vfnew(i,j-1))

What confuses me is I am quite certain my PPE solver is 100% correct. My PPE solver is as follows

subroutine PressureSolver (P, us, vs, un, vn)
    implicit none
    integer :: i, j
    double precision, dimension(nx,ny), intent(out) :: P
	double precision, dimension(nx,ny), intent(in) :: us, vs
    double precision, dimension(nx,ny), intent(in) :: un, vn
	double precision, dimension(nx,ny) :: vfs, ufs
	double precision, dimension(nx,ny) :: R, Res
	double precision, parameter :: inv_dxx = 1.0/dx**2.0
	double precision, parameter :: inv_dyy  = 1.0/dy**2.0
	double precision, parameter :: inv_dx = 1.0/dx
	double precision, parameter :: inv_dy = 1.0/dy
    double precision, parameter :: tol = 1e-6
    double precision, parameter :: iter_max = 16000
    double precision, parameter :: omega = 1.96
    double precision :: L2_Error
    integer :: it

    call FaceVelocities(us,vs,ufs,vfs)

    do j=3,ny-2
        do i=3,nx-2
            R(i,j) = (rho/dt)*(inv_dx*(ufs(i,j) - ufs(i-1,j)) + inv_dy*(vfs(i,j) - vfs(i,j-1)))
        end do
    end do

    it = 0

    do while (it <= iter_max)
        do j=3,ny-2
            do i=3,nx-2
                P(i,j) = (1.0-omega)*P(i,j) + omega/(2.0*inv_dxx + 2.0*inv_dyy)*(inv_dxx*(P(i+1,j) + P(i-1,j)) + inv_dyy*(P(i,j+1) + P(i,j-1)) - R(i,j))
            end do
        end do

        do j=3,ny-2
            R(2,j) = (rho/dt)*(inv_dx*(ufs(2,j)- un(1,j)) + inv_dy*(vfs(2,j) - vfs(2,j-1)))
            P(2,j) = (1.0-omega)*P(2,j) + omega/(inv_dxx + 2.0*inv_dyy)*(inv_dxx*P(3,j) + inv_dyy*(P(2,j+1) + P(2,j-1)) - R(2,j))

            R(nx-1,j) = (rho/dt)*(inv_dx*(un(nx,j) - ufs(nx-2,j)) + inv_dy*(vfs(nx-1,j) - vfs(nx-1,j-1)))
            P(nx-1,j) = (1.0-omega)*P(nx-1,j) + omega/(inv_dxx + 2.0*inv_dyy)*(inv_dxx*P(nx-2,j) + inv_dyy*(P(nx-1,j+1) + P(nx-1,j-1)) - R(nx-1,j))
        end do

        do i=3,nx-2
            R(i,2) = (rho/dt)*(inv_dx*(ufs(i,2) - ufs(i-1,2)) + inv_dy*(vfs(i,2)- vn(i,1)))
            P(i,2) = (1.0-omega)*P(i,2) + omega/(2.0*inv_dxx + inv_dyy)*(inv_dxx*(P(i+1,2) + P(i-1,2)) + inv_dyy*P(i,3) - R(i,2))

            R(i,ny-1) = (rho/dt)*(inv_dx*(ufs(i,ny-1)- ufs(i-1,ny-1)) + inv_dy*(vn(i,ny) - vfs(i,ny-2)))
            P(i,ny-1) = (1.0-omega)*P(i,ny-1) + omega/(2.0*inv_dxx + inv_dyy)*(inv_dxx*(P(i+1,ny-1) + P(i-1,ny-1)) + inv_dyy*P(i,ny-2) - R(i,ny-1))
        end do

        R(2,ny-1) = (rho/dt)*(inv_dx*(ufs(2,ny-1) - un(1,ny-1)) + inv_dy*(vn(2,ny) - vfs(2,ny-2)))
        P(2,ny-1) = (1.0-omega)*P(2,ny-1) + omega/(inv_dxx + inv_dyy)*(inv_dxx*P(3,ny-1) + inv_dyy*P(2,ny-2) - R(2,ny-1))

        R(nx-1,2) = (rho/dt)*(inv_dx*(un(nx,2) - ufs(nx-2,2)) + inv_dy*(vfs(nx-1,2) - vn(nx-1,1)))
        P(nx-1,2) = (1.0-omega)*P(nx-1,2) + omega/(inv_dxx + inv_dyy)*(inv_dxx*P(nx-2,2) + inv_dyy*P(nx-1,3) - R(nx-1,2))

        R(nx-1,ny-1) = (rho/dt)*(inv_dx*(un(nx,ny-1) - ufs(nx-2,ny-1)) + inv_dy*(vn(nx-1,ny) - vfs(nx-1,ny-2)))
        P(nx-1,ny-1) = (1.0-omega)*P(nx-1,ny-1) + omega/(inv_dxx + inv_dyy)*(inv_dxx*P(nx-2,ny-1) + inv_dyy*P(nx-1,ny-2) - R(nx-1,ny-1))

        R(2,2) = (rho/dt)*(inv_dx*(ufs(2,2) - un(1,2)) + inv_dy*(vfs(2,2) - vn(2,1)))
        P(2,2) = (1.0-omega)*P(2,2) + omega/(inv_dxx + inv_dyy)*(inv_dxx*P(3,2) + inv_dyy*P(2,3) - R(2,2))

        do j=3,ny-2
        	do i=3,nx-2
    			Res(i,j) = (inv_dxx*(P(i-1,j) - 2.0*P(i,j) + P(i+1,j)) + inv_dyy*(P(i,j-1) - 2.0*P(i,j) + P(i,j+1))) - R(i,j)
        	end do
        end do

        L2_Error = 0.0

        do j=3,ny-2
        	do i=3,nx-2
                L2_Error = L2_Error + sqrt(dx*dy*abs(Res(i,j)*Res(i,j)))
            end do
        end do

        if (L2_Error >= tol) then
          it = it + 1
        else
            print *, "PPE has converged", it
            print *, "L2_Error = ", L2_Error
        	exit
        end if
    end do

    do j=1,ny
        P(1,j) = P(2,j) + (dx/dt)*(us(1,j) - un(1,j))
        P(nx,j) = P(nx-1,j) - (dx/dt)*(us(nx,j) - un(nx,j))
    end do

    do i=1,nx
        P(i,1) = P(i,2) + (dy/dt)*(vs(i,1) - vn(i,1))
        P(i,ny) = P(i,ny-1) - (dy/dt)*(vs(i,ny) - vn(i,ny))
    end do
    return
end subroutine PressureSolver

[FMDenaro]

I need to know how you collocated the velocity components ufnew,vfnew and us,vs and P

[selig5576]

So I am collocated ufnew, vfnew as such

do j=2,ny-1
        do i=2,nx-1
            ufnew(i,j) = 0.5*(us(i+1,j) + us(i,j)) - (dt/rho)*(P(i+1,j) - P(i,j))
            vfnew(i,j) = 0.5*(vs(i,j+1) + vs(i,j)) - (dt/rho)*(P(i,j+1) - P(i,j))

            cont(i,j) = (1.0/dx)*(ufnew(i,j) - ufnew(i-1,j)) + (1.0/dy)*(vfnew(i,j) - vfnew(i,j-1))
        end do
    end do

In other words





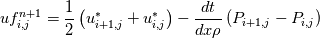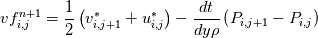This is also used to construct the PPE (Rhie-Chow method).

[FMDenaro]

According to your notation, us, vs, P are co-located while uf(i,j) is staggered at i+1/2 and vf(i,j) at j+1/2.

Considering only the x-component, you have

(1.0/dx)*(ufnew(i,j) - ufnew(i-1,j))=

(1.0/dx)*(0.5*(us(i+1,j) + us(i,j)) - (dt/rho)*(P(i+1,j) - P(i,j))
- 0.5*(us(i,j) + us(i-1,j)) + (dt/rho)*(P(i,j) - P(i-1,j)))

That leads to the standard Poisson equation. But at the boundary you have to impose the correct velocity,
for example at the inflow you substitute the physical velocity ufnew(i-1,j)=uinflow so that

(1.0/dx)*(ufnew(i,j) - ufnew(i-1,j))=

(1.0/dx)*(0.5*(us(i+1,j) + us(i,j)) - (dt/rho)*(P(i+1,j) - P(i,j))
- uinflow)

[Dave110]

Hi Selig,

I am working on DNS of free circular round jet for Re=1000 to 2000.

At the inlet you can go for velocity profile suggested by Michalke et al. (Tan hyperbolic profile). which is good approximation of velocity profile in near field region of the jet.

[selig5576]

Dr. Denaro,

I agree, however I believe I am already doing this when I solve the PPE at the boundary:





In this case as I have an outflow BC. I could be wrong, but I do not set this in the PPE, but rather when I set the boundary conditions for .