 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Jory
Join Date: Apr 2017
Location: Canada
Posts: 4
Rep Power: 9  |
Hey guys,
I'm currently trying to implement a decoupled finite-rate chemistry solver, which solves a set of species conservation equations: 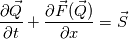 where 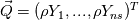 and 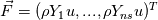 I seem to be having convergence issues and I believe it may be an issue with the stabilization scheme. I'm using Roe's flux difference scheme, where the fluxes are basically given by: 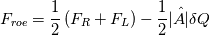 Where the A matrix is the flux Jacobian made using Roe's averaged variables and delta Q is the difference in solution variables from right to left. It is my understanding that, in the absence of source terms, the equations are completely decoupled from each other, as well as being decoupled from the flow system. Furthermore, since the flow variables are simply the species densities, and the fluxes are the species densities multiplied by the velocity, the flux jacobian is simply a diagonal matrix with the velocity on the diagonal. If anyone has experience with this, does this formulation seem correct? |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,896
Rep Power: 73    |
yes, the equations are decoupled as you can see from the k-th equation
d(rho*Yk)+d(u*rho*Yk)/dx=0 that means that rho*Yk varies along the pathline dx/dt=u if u depends on x, according to D(rho*Yk)/Dt = - (rho*Yk)*du/dx |
|
|
|

|
|
|
|
|
#3 |
|
Super Moderator
|
How are you actually computing the flux for the species ? Its not clear from your post.
One way is to use the mass flux given by the Roe scheme and make an upwind flux out of that for the species transport. If the mass flux is 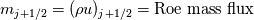 then the specifies flux is 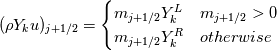 Here 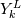 , , 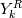 are the reconstructed values at the face. are the reconstructed values at the face.
|
|
|
|

|
|
|
|
|
#4 |
|
New Member
Nikhil
Join Date: Mar 2016
Location: India
Posts: 15
Rep Power: 10  |
Dear Friend,
Before we start scheme suggested in above comment is a upwind scheme. As we know flow characteristic variables is different in compressible flow from its in-compressible counterpart. Use of such upwind scheme is not recommended as it is based on only wave speed U. (Acoustic wavesa and entropy are ignored) There is one of the major implementation issue with Roe scheme for chemical reaction is that the constriction of Roe matrix which is there in net flux. I'm summarizing few issues and their solution. 1) We generally solve for N-1 species instead of N species while dealing with chemical reaction, because there is linear dependency between N species equation with continuity equation system i.e local coefficient matrix becomes singular, instead we can solve for N-1 species and get Nth species from that. There are other physical reasons such as diffusion has summed to be zero and so many. This singularity is problem mainly with implicit schemes for explicit schemes as we march directly there is no such issue. 2) Form of equation of state for N-1 species is different form its usual form because of which there is need to re-derive expression for Roe matrix because of change in expression of ideal gas equation (it's same equation written for N-1 species not for N species). Check this paper http://www.sciencedirect.com/science...2199919090172W 3) Reacting flow are usually at low mach (in compressible limit) and when you deal with Roe scheme for low speed flows you are advised to preconditioning or any other scheme from all-speed family. 4) Conclusion is direct extension of Roe scheme for chemically reacting flows is not straight. Simpler solution is to use the AUSM based schemes which can be easily extended for species transport. There is newest scheme in AUSM family called SLAU, SLAU-2, SLAU-HR which also take care of stiffness happened because of low speed and one has not to worry about preconditioning. I have implemented SLAU scheme in our in-house solver and and worked well so far. |
|
|
|

|
|
 |
| Tags |
| chemistry, roe, stabilization |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Central-upwind scheme for two-layer shallow water equations | Wubbalubbadubdub | Main CFD Forum | 0 | January 18, 2017 19:34 |
| Best numerical scheme for MHD wave equations | peich | Main CFD Forum | 0 | April 17, 2013 08:55 |
| Roe scheme for general equation of state | zouchu | Main CFD Forum | 3 | August 10, 2000 17:46 |
| Crank-Nicolson technique for Conservation form of equations | Yogesh Talekar | Main CFD Forum | 2 | July 20, 1999 02:45 |
| CONSERVATION EQUATIONS IN NONINERTIAL SYSTEM!!! | zhang zhanwang | Main CFD Forum | 0 | August 17, 1998 08:38 |