 |
|
|
[Sponsors] | |||||
How to compute WENO-reconstructed flux in local characteristic field? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
I'm trying to apply finite-difference characteristic-wise WENO method to 1D Euler equations:
 Physical values are set at grid points  , so we need to approximate fluxes at mid-points , so we need to approximate fluxes at mid-points  : :![U_t \approx \frac{1}{h} \left[ \widehat{f}_{j+\frac{1}{2}} - \widehat{f}_{j-\frac{1}{2}} \right] U_t \approx \frac{1}{h} \left[ \widehat{f}_{j+\frac{1}{2}} - \widehat{f}_{j-\frac{1}{2}} \right]](/Forums/vbLatex/img/1a5ef58f65757fa58c2be87fc474e850-1.gif) where  are sought-for approximation of physical fluxes are sought-for approximation of physical fluxes  . .My algorithm is the following: 1) For each  , we calculate simple average state , we calculate simple average state  and, using it, local eigenvalues and, using it, local eigenvalues  , right eigenvector matrix , right eigenvector matrix  and it's left counterpart and it's left counterpart  . (Subscript . (Subscript  will be omitted below) will be omitted below)2) Now we transform 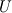 , its differences , its differences  and flux differences and flux differences  to local characteristic field: to local characteristic field: It is done only for relevant grid points which in my case (  ) are ) are  . .3) Then we reconstruct characteristic variable values by WENO method using  , ,  and and  . We get two "candidates": . We get two "candidates": where  are a convex combinations of corresponding polynomial functions obtained by WENO method. are a convex combinations of corresponding polynomial functions obtained by WENO method.The next step would be to compute 2-point flux function  using these reconstructed values. I'm using Lax-Friedrich's function: using these reconstructed values. I'm using Lax-Friedrich's function:![h(a,b) = \frac{1}{2} \left[ F(a) + F(b) + \alpha(b-a) \right] h(a,b) = \frac{1}{2} \left[ F(a) + F(b) + \alpha(b-a) \right]](/Forums/vbLatex/img/e6961cc02d99a02b358483a05033e842-1.gif) where 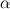 is maximum value of eigenvalue (different for each of equations, since they are decoupled now). is maximum value of eigenvalue (different for each of equations, since they are decoupled now).But how to compute these  and and  using using  ? In component-wise approach it is simple: we reconstruct base values - ? In component-wise approach it is simple: we reconstruct base values -  , for example - and the use explicit formulas to compute , for example - and the use explicit formulas to compute  and and  , but we don't have such formulas for , but we don't have such formulas for  because because  is expressed in local characteristic field... is expressed in local characteristic field...
|
|
|
|

|
|
|
|
|
#2 |
|
Member
Oleg Sutyrin
Join Date: Feb 2016
Location: Russia
Posts: 41
Rep Power: 10  |
It seems that I was misunderstanding how the flux is reconstructed:
My idea was to reconstruct base values - 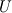 (or (or  if we are performing characteristic decomposition) - and then substitute them to formulas of if we are performing characteristic decomposition) - and then substitute them to formulas of  (or (or  ) to obtain reconstructed fluxes. ) to obtain reconstructed fluxes. It looks like the correct way is to apply reconstruction procedure to  (or (or  which is obtained by transformation which is obtained by transformation  ) itself. Some quick tests I performed with this approach show very plausible results. ) itself. Some quick tests I performed with this approach show very plausible results.
|
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Hi there,
Here's what I am doing: after reconstructing the characteristic variables at the face, I use the left eigenvector matrix to convert them back to primitive variables. Then, I use these to compute the flux using the flux function, e.g. Lax-Friedrich method. It has performed well in several 1D test cases. USV |
|
|
|

|
|
 |
| Tags |
| charateristic-wise, finite-difference, weno |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| p_rgh initial residual no change with different settings | manuc | OpenFOAM Running, Solving & CFD | 3 | June 26, 2018 16:53 |
| Moving mesh | Niklas Wikstrom (Wikstrom) | OpenFOAM Running, Solving & CFD | 122 | June 15, 2014 07:20 |
| Problem with rhoSimpleFoam | matteo_gautero | OpenFOAM Running, Solving & CFD | 0 | February 28, 2008 07:51 |
| Convergence moving mesh | lr103476 | OpenFOAM Running, Solving & CFD | 30 | November 19, 2007 15:09 |
| IcoFoam parallel woes | msrinath80 | OpenFOAM Running, Solving & CFD | 9 | July 22, 2007 03:58 |