 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Leonhard Schmalhorst
Join Date: Nov 2015
Location: Munich, Germany
Posts: 1
Rep Power: 0  |
Hi everyone,
I'm trying to set up a solver in matlab for gas flowing through a fixed bed reactor. The equations i have are the momentum balances in axial and in radial direction and the mass continuity equation. So far, so good... My proceeding is as follows:
Obviously, the steps 1-3 are the same as in nearly all algorithms. But since my algorithm does not work (oscillating residuals) i am not sure if steps 4 - 7 are correct. Does anyone has an advice for me? I'm thankful for every answer. Have a nice weekend, Cheers, Leo PS: Here are the equations i'm using: Momentum balance radial direction: 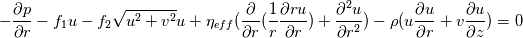 Momentum balance axial direction: 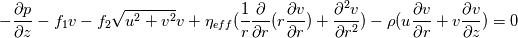 Continuity equation: 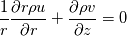 Ideal gas law: 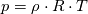
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Michael Prinkey
Join Date: Mar 2009
Location: Pittsburgh PA
Posts: 363
Rep Power: 25  |
Are your linear solutions for velocity components and density converging well at all stages of convergence?
Are your velocity components collocated with your pressure and density data? Are you under-relaxing your velocity and pressure corrections? If your fields are collocated, you may have a pressure-velocity-density coupling problem. That can be fixed with either staggered grid configurations or Rhie-Chow interpolation for pressure. If you are not under-relaxing your pressure and velocity corrections, you likely need to. Or, perhaps, you need to use a pseudo-transient formulation and pseudo-time march to your solution. This is a common solution procedure for steady compressible flows. If your linear systems solutions are not converging well, you may need to do implicit under-relaxation to effectively solve for the relaxed velocity/density correction and generate a more diagonal dominate linear system that converges more quickly/robustly. Good luck. |
|
|
|

|
|
|
|
|
#3 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,761
Rep Power: 66    |
Leo, you have basically written down how to solve the continuity & momentum equations in a segregated approach (there's no energy equation). The approach is sound but you will likely have convergence difficulties due to the pressure-velocity coupling problem. Your steps 1-7 will become much more complicated. It's non-trivial how you go about solving this problem, but basically you need lots of under-relaxation.
The problem is that after step #5, you momentum equation will no longer be satisfied (it is almost guaranteed, unless your simulation has already converged). This is why there are algorithms like SIMPLE & PISO to make an additional velocity/pressure adjustment. Or you will have to solve steps 2-6 iteratively. Btw in step #5, actually you also assume an initial temperature field in step #1. Solving the energy equation and any other transport equations should not be in the loop of steps 1-7 but a separate routine altogether. As soon as you try to bring in the energy equation, your problem becomes coupled and you have to solve one big matrix and solve for u, rho, p, and T simultaneously. The steps for solving that big system are very different. |
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Join Date: Aug 2011
Posts: 272
Rep Power: 16  |
Hi Istum,
In your model you do not solve the energy equation which is a relevant part of the compressible fluid flow model. I'm not sure you can solve an isothermal compressible flow, because as density and pressure change, the temperature should change too. In case the flow is really isothermal, the energy equation should simulate this characteristic. Thus it might explain your convergence problem. If you aim to solve a compresssible flow you do not need to staggered your velocity. You can work with colocated variables and without the necessity to use RC interpolation. the overall algorithm reads as follow see the attached jpg file: Writting a code based on this algorithm is really simple. Less than 1000 lines using finite differences. You do not need internal sweeping between two consecutive time steps. This is very efficient. Leflix |
|
|
|

|
|
 |
| Tags |
| compressible, fixed bed, gas, pressure correction |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Wind tunnel Boundary Conditions in Fluent | metmet | FLUENT | 6 | October 30, 2019 13:23 |
| SIMPLE algorithm does not converge when using old pressure (correction) values | andreasp | Main CFD Forum | 3 | February 9, 2016 22:18 |
| Gas Diffusion and Pressure Distribution | Xuekun | Main CFD Forum | 0 | October 29, 2015 11:10 |
| Using ideal gas law to simulate pressure decline | Björn Mattsson | FLUENT | 5 | September 5, 2005 05:03 |
| Hydrostatic pressure in 2-phase flow modeling (long) | DS & HB | Main CFD Forum | 0 | January 8, 2000 16:00 |