 |
|
|
[Sponsors] | |||||
Implicit discretization of Jacobian term in FV: Construction of Coefficient matrix |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
Senior Member
Santiago Lopez Castano
Join Date: Nov 2012
Posts: 354
Rep Power: 16  |
I am currently trying to write the linear system coefficients of the following system:
 But I cannot get my head around on how to come up with the coefficients for the jacobian fluxes. I mean, I see a tensor that needs to be projected along $\mathbf{n}$ and from it you do the discretization. My attempt on this enterprise is (the simplest, I think):  What makes me uneasy is the fact that  is a vector. Thus, Are the coefficients for each of the vector's components equal to the face-normal projected distance between the neighboring centroids? is a vector. Thus, Are the coefficients for each of the vector's components equal to the face-normal projected distance between the neighboring centroids?
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
I do not understand your symbolism...
1) the first term in the LHS is the time derivative of u?? 2) Since the first term is a vector, the second term in the LHS is the integral of a tensor (uu??) projected along the normal unit vector to the surface n. For example, Int [S] n.uu dSIn your equation the symbol du/dn is still a tensor (why is d(du)?). The Jabian of the flux can be derived from the differential form starting from df/dxi = (df/dui)*(dui/dxi) |
|
|
|

|
|
|
|
|
#3 | |
|
Senior Member
Santiago Lopez Castano
Join Date: Nov 2012
Posts: 354
Rep Power: 16  |
Quote:
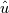 , ,  it's just a vector. Besides the equation is already discrete in time. it's just a vector. Besides the equation is already discrete in time.2.) The the second term is just a diffusion transformed in a flux using the green-gauss theorem. What I want is to get the coefficients of A, for the system: ![[A][d\hat{\mathbf{u}}] = [R(\mathbf{u})] [A][d\hat{\mathbf{u}}] = [R(\mathbf{u})]](/Forums/vbLatex/img/23ab91bef4d40272d9366da7afd1411d-1.gif) Part of the diagonal terms are given by the first term of LHS, but my question is how to discretize the second term. Thanks. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
thus, using Gauss you have a surface integral like
Int [S] n. grad u dS why do you need to introduce a Jacobian? you can directly discretize the integral of the fluxes |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Santiago Lopez Castano
Join Date: Nov 2012
Posts: 354
Rep Power: 16  |
I referred the derivative of the vector function as jacobian. My bad.
Sent from my GT-I8190L using CFD Online Forum mobile app |
|
|
|

|
|
 |
| Tags |
| finite volume method, linear system |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Question about heat transfer coefficient setting for CFX | Anna Tian | CFX | 1 | June 16, 2013 07:28 |
| ATTENTION! Reliability problems in CFX 5.7 | Joseph | CFX | 14 | April 20, 2010 16:45 |
| FVM discretization of diffusion term on crvlnr gr | Michail | Main CFD Forum | 3 | March 14, 2008 07:52 |
| Convection Term Discretization | Maciej Matyka | Main CFD Forum | 3 | October 7, 2004 05:32 |
| Coefficient matrix | Question. | Main CFD Forum | 1 | September 12, 2004 22:19 |