 |
|
|
[Sponsors] | |||||
|
|
|
#1 |
|
New Member
Join Date: Apr 2016
Posts: 4
Rep Power: 10  |
Hello guys,
I have a question to a waterflow simulation, lets consider its 2D. In an area with a no flow boundary condition, water flows stationary from points with high potential to points with low potential. The equation to be solved is the incompressible source-free mass conservation equation, in which the velocity can be expressed as product of hydraulic conductivity and the gradient of the potential (pressure head), following Darcys law. Its the standard groundwater flow equation. At some points the pressure head is known and set constant for the time of iteration. As result i get a nice velocity field and streamlines of the water flow. But there is one problem. At the points with constant pressure head, mass balance is not zero. Thats clear, because water flows for example only out of the cell, leaving a deficit of mass. No water leaves or entries the geometry because of the no flow boundary condition. My question is how to solve the geometry in a correct way, only with the help of the known pressure heads. What other boundary conditions are possible? Do i have to iterate multiple times with changing boundary conditions? Thanks |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
I suggest to give us more details of your setting, geometry, grid and BC. |
||
|
|

|
||
|
|
|
#3 |
|
New Member
Join Date: Nov 2014
Posts: 2
Rep Power: 0  |
Hey thanks for your reply. Pls ignore the different user name.
I made a picture to show my area. Its a view from above. At the boundary there is no flow. The cells at h_1 (in between thick line) have a high pressure head, the cells with h_2 have a low potential. Because there is no flow on the left and on the right, there will be regions with same potential (dark red, dark blue). There is no groundwater flow. In between the different pressure heads cause a horizontal flow from red to blue. Thats what solving my mass conservation equation does ( div(k grad h) = 0 ). If i do my mass balance in one of the dark red cells (yellow), there is an outflow but no inflow, what means that water comes out of nowhere. The mass balance in the middle region (green) yields to a correct mass balance. I want to introduce a boundary condition where there is a physically senseful flow coming from the boundary, without knowing mass fluxes on the boundary. Only with my pressure heads. 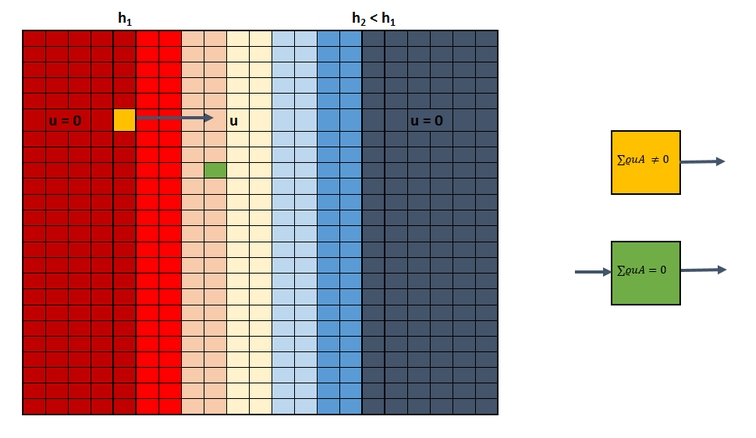
|
|
|
|

|
|
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
I never worked on this kind of flow problem, I do not fully understand your problem ...
if u=0 is forced on a face of the cell, the continuity equation will be satisfied by a vertical variation of the velocity that balances the horizontal one. Why are you thinking like a one-dimensional problem? |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Join Date: Apr 2016
Posts: 4
Rep Power: 10  |
Thanks for your reply.
Maybe i can say it with an analogy. I have a room with stationary temperature distribution and measure my temperature at two points in the room. As result i get one point with a high temperature eg 20°C and one point with 18°C. Now i want to know what the other temperatures in my room are using numerical methods. Considering its only heat conduction without sources, i can use the heat conduction equation div q = 0; div (k grad T) = 0, setting the two known points with constant temperature. If i say its a perfectly isolated room my heat fluxes normal through the boundary is zero: grad T = 0. What i get after solving is a temperature distribution where the temperature in the room lies between 18 and 20°C. Now if i do my energy conservation balance somewhere in the field it will give me 0, thats what to expect by solving the laplacian equation. If i do my balance on the cell with constant 20°C, there will be only heat fluxes leaving the cell, because it has the highest temperature in the room. So energy balance is not satisfied. That problem is caused by my boundary conditions. To satisfy my energy balance there must be heat fluxes coming in and going out the boundary. On the boundary there must exist a temperature higher than 20°C. But what bconditions do i have to use without knowing the exact heatflux on the boundary (neumann condition). Do i have to solve my equation system multiple times with changing my boundary conditions iterative? Or are there maybe infinite solutions to this problem? Thank you |
|
|
|

|
|
|
|
|
#6 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,865
Rep Power: 73    |
Quote:
Sorry, I still have doubts.... the case you are setting produces a volume dilatation since v=0 in the vertical direction and du/dx is not. Consequently, you must consider the time variation du/dt to balance the momentum and the mass equation for compressible flows. Conversely, I believe you need to focus on the fact that for incompressible flows, fixing only the pressure as BC does not force the velocity at the boundary to be zero. It is a classical condition used for example in the outlet of channel where you can fix the value of the pressure and let the velocity to adjust to fulfill the mass equation. The only task is to set some numerical condition for the velocity that accords the best to the physics of the problem. For example a fully developed outflow can be quite accurately described by homogeneous Neuman condition. In conclusion, I can suggest to try some condition on the velocity derivative and then check the mass balance. But I suspect that your problem requires somehow a compressible unsteady model. |
||
|
|

|
||
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Natural Convection heat transfer problem | srinivasa | FLUENT | 21 | November 11, 2016 07:08 |
| interfoam: a problem with removing convection in the air phase | bieshuxuhe | OpenFOAM | 0 | March 31, 2014 23:56 |
| Problem to simulate conduction and convection in the same time in FLUENT | zomayabssa | FLUENT | 0 | March 1, 2014 23:33 |
| natural convection problem | samantasubho | FLUENT | 0 | October 6, 2010 11:07 |
| ON TURBULET MODEL FOR A NATURAL CONVECTION PROBLEM | varghese | FLUENT | 6 | February 6, 2002 06:23 |