 |
|
|
[Sponsors] | |||||
Problems implementing axisymmetric Method of Characteristics |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Pedro Nascimento
Join Date: Jun 2016
Posts: 1
Rep Power: 0  |
Hi
I'm currently trying to implement the method of characteristics for axisymmetric irrotational compressible flow as part of a project of implementing Rao's method for the design of optimum thrust nozzle contours, but I've ran into some issues I hope you can shed some light on. We have the following governing equations:   Which yields the following characteristic equation:  And the following compatibility relation which is valid along the mach lines: ![(u^{2}-a^{2})du_{\stackrel{+}{-}}+[2uv-(u^{2}-a^{2})\lambda_{\stackrel{+}{-}}]dv_{\stackrel{+}{-}}-(a^{2}v/y)dx_{\stackrel{+}{-}} (u^{2}-a^{2})du_{\stackrel{+}{-}}+[2uv-(u^{2}-a^{2})\lambda_{\stackrel{+}{-}}]dv_{\stackrel{+}{-}}-(a^{2}v/y)dx_{\stackrel{+}{-}}](/Forums/vbLatex/img/702686290911880bf782173bab575e54-1.gif) My issue is when implementing the unit process for an interior point, if the point from which the left-running characteristic originates sits on the axis of symmetry, the term  goes to infinity, so how should I treat this equation, should I consider that the whole term goes to infinity, so how should I treat this equation, should I consider that the whole term  goes to zero, since on the symmetry axis we also have goes to zero, since on the symmetry axis we also have  ? ?Thank you, Pedro N 
|
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Join Date: Sep 2015
Location: Singapore
Posts: 102
Rep Power: 11  |
Hi Pedro,
I am new to MOC myself but I have developed my own code for planar MOC successfully and I am trying to develop my own code for axisymmetric MOC as well. I just thought we could help each other. To answer your question: No, the term  does not go to 0 in the limit of does not go to 0 in the limit of  . It approaches . It approaches  . So, if you have a point very close to the axis where you know . So, if you have a point very close to the axis where you know  and and 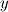 , you can probably approximate the term by , you can probably approximate the term by  . .I am facing a similar problem actually. I am working with the Mach number  and the flow angle and the flow angle 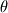 as my variables as opposed to as my variables as opposed to  and and  . Given the throat height (or mass flow rate) and design Mach number, how do you set up the initial conditions to kick-start the solution process? Unlike the planar case, the Riemann invariants . Given the throat height (or mass flow rate) and design Mach number, how do you set up the initial conditions to kick-start the solution process? Unlike the planar case, the Riemann invariants  do not remain constant along the characteristics. So, how do you set up the starting characteristic when you have no characteristics to intersect it? do not remain constant along the characteristics. So, how do you set up the starting characteristic when you have no characteristics to intersect it?Many thanks. |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| LatticeBoltzmann method for axisymmetric flows | grissa | Main CFD Forum | 0 | February 14, 2015 05:32 |
| Help regarding implementing the Finite Volume method for meridional flows | shreyasr | Main CFD Forum | 0 | July 23, 2012 08:05 |
| Problem with implementing unsteady Kutta condition-Hess and Smith Panel method | samarthgk.nitk | Main CFD Forum | 0 | June 25, 2012 03:36 |
| Has the pressure correction method problems? | X. Ye | Main CFD Forum | 17 | September 1, 1999 17:14 |
| Want someone to discuss regarding ADADTIVE GRID METHODOLOGY AND THE METHOD OF CHARACTERISTICS. | RAGHURAM K.S | Main CFD Forum | 1 | February 15, 1999 13:21 |