 |
|
|
[Sponsors] | |||||
How can I calculate momentum efflux from boundary data of a 2D nozzle? |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
gautham narayan
Join Date: Apr 2015
Posts: 16
Rep Power: 11  |
I am trying to calculate the momentum efflux(N/m) from a 2d axis-symmetric case of a CD nozzle. I have the U,V momentums and pressure data. I have tried to use trapezoidal rule to line integrate the momentum at the exit. This is resulting in extremely low values. There might be an error in the variables I am integrating.
Can someone please guide me as to how I could calculate the momentum efflux from the boundary data of a 2D case. |
|
|
|

|
|
|
|
|
#2 | |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
|
||
|
|

|
||
|
|
|
#3 | |
|
New Member
gautham narayan
Join Date: Apr 2015
Posts: 16
Rep Power: 11  |
Quote:
Dear sir, I have the UMomentum from the solver. I have tried to integrate 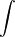 Pdx using the trapezoidal rule. If this is correct, then I have a fundamental doubt. Please bear with me as it may seem obvious. Pdx using the trapezoidal rule. If this is correct, then I have a fundamental doubt. Please bear with me as it may seem obvious.The units of momentum efflux is N/m. which I have understood as Force/unit length of boundary. But, Force = Momentum/Time Please can you explain how integral of momentum with length, gives a result in N/m. Thank you very much. |
||
|
|

|
||
|
|
|
#4 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,849
Rep Power: 73    |
Quote:
As you see, the momentum flux has the dimension of the pressure (N/m^2) therefore just a line integration gives dimension (N/m) |
|
|
|

|
|
|
|
|
#5 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,747
Rep Power: 66    |
||
|
|

|
|
|
|
|
#6 | |
|
New Member
gautham narayan
Join Date: Apr 2015
Posts: 16
Rep Power: 11  |
Quote:
I am using a cartesian coordinate system. I was actually of by a huge factor. Anyways I was able to solve it. Turns out i was supposed to also multiply it with velocity. This particular solver outputs momentum as rho*u and not rho*u*u. So actually i was ending up with mass flow integral and not that of momentum efflux. Thanks for your reply. |
||
|
|

|
||
|
|
|
#7 |
|
Senior Member
Lucky
Join Date: Apr 2011
Location: Orlando, FL USA
Posts: 5,747
Rep Power: 66    |
That's great. I guess as a final note for others that might read this thread in the future I'd like to point out:
If you are talking about a particular fluid particle at a given location r(x,y,z) then rho*u is the momentum of the fluid particle at that location. So it is correct to say that rho*u is the momentum of a fluid particle. The confusion is when you integrate fluxes through an area element dA, there is a dot products of the velocity vector with the area vector dA. i.e. mass flux is the integral of simply rho, the rate of efflux of mass density is mass flux which is then the product of rho with the dot product of u and dA. It's important to differentiate what is the property being advected (rho for mass, rho*u for momentum, rho*h for enthalpy) and the rate at which it is being advected (u dotted with dA). |
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Setting the height of the stream in the free channel | kevinmccartin | CFX | 12 | October 13, 2022 22:43 |
| GETVAR Error in Multiband Monte Carlo Radiation Simulation with Directional Source | silvan | CFX | 3 | June 16, 2014 10:49 |
| Modeling interface of fluid and porous, not with default setting | ftab | CFX | 27 | May 20, 2014 07:58 |
| RPM in Wind Turbine | Pankaj | CFX | 9 | November 23, 2009 05:05 |
| How to update polyPatchbs localPoints | liu | OpenFOAM Running, Solving & CFD | 6 | December 30, 2005 18:27 |