 |
|
|
[Sponsors] | |||||
Effect of discretization of viscous terms (FVM) for incompressible fluids on pressure |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 12  |
According to Perić's book (Computational Methods for Fluid Mechanics 3rd. Ed. p. 158) when discretizing the viscous term of the incompressible Navier-Stokes equations
![\frac{\partial}{\partial x_j} \left[\mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) \right] \frac{\partial}{\partial x_j} \left[\mu \left( \frac{\partial u_i}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) \right]](/Forums/vbLatex/img/8f562305d4f8416d266886930a81701b-1.gif) one can use the fact, that for flows with spatially invariant viscosity 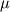 the second term will not contribute to the viscous term. This follows from the linearity of the derivation, interchange of the differentiation order and finally the application of the continuity equation for incompressible fluids the second term will not contribute to the viscous term. This follows from the linearity of the derivation, interchange of the differentiation order and finally the application of the continuity equation for incompressible fluids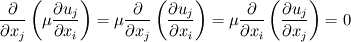 My solver application, which is based on Perić's CAFFA code, is able to choose between both approximations. I solve for a manufactured solution (2d Taylor-Green vortex) with Dirichlet boundaries and I experience a notable difference in the resulting discretization error depending on the decision to use the aforementioned simplification or not. Without the simplification the discretization error is about 10 times bigger. Even more confusing is the calculated pressure, which I attached. I don't understand why the pressure would look so different in the boundary control volumes. Have you seen something similar before and can tell me, if there is something wrong with my code? The pressure has been extrapolated with a zero order profile at the boundaries. |
|
|
|

|
|
|
|
|
#2 |
|
Senior Member
Filippo Maria Denaro
Join Date: Jul 2010
Posts: 6,897
Rep Power: 73    |
as the identity requires Div v = 0, I suppose you can have some high residual in the continuity equation.
Furthermore, do not use the absolute pressure but its gradient as comparison terms |
|
|
|

|
|
|
|
|
#3 |
|
New Member
Fabian Gabel
Join Date: Oct 2014
Location: Darmstadt
Posts: 13
Rep Power: 12  |
I checked the residual of the continuity equation (right hand side of the pressure correction) and it is low (1.7269e-09). Furthermore continuity seems to be preserved locally, since each line of the linear system has an almost zero right hand side coefficient (maximum absolute value: 1.9118e-10).
Checking the pressure gradients shows the same strange behavior at the domain boundaries, I attached the results, the left plot represents the calculation using the simplification of the diffusive term. What seems to be contradicting the fact that the residual of the continuity equation is low, can be seen in the third attachment. I calculated the additional contribution  for each cell , for each cell ,  being the face normal unit vector and being the face normal unit vector and  being the surface area, and it doesn't vanish at all at certain domain boundaries. being the surface area, and it doesn't vanish at all at certain domain boundaries.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| Calculation of the Governing Equations | Mihail | CFX | 7 | September 7, 2014 07:27 |
| Neumann pressure BC and velocity field | Antech | Main CFD Forum | 0 | April 25, 2006 03:15 |
| Implicitisation of viscous terms | Michael Halls-Moore | Main CFD Forum | 0 | April 3, 2006 08:52 |
| what the result is negatif pressure at inlet | chong chee nan | FLUENT | 0 | December 29, 2001 06:13 |
| K-Epsilon model? | Brindaban Ghosh | Main CFD Forum | 2 | June 24, 2000 05:22 |