 |
|
|
[Sponsors] | |||||
coupling vof with single phase flow and gravity term |
 |
|
|
LinkBack | Thread Tools | Search this Thread | Display Modes |
|
|
|
#1 |
|
New Member
Kareem
Join Date: Mar 2012
Posts: 9
Rep Power: 14  |
Hey everyone,
currently developing two phase flow solver. I have written a 2D navier stokes solver for a single phase flow and tested it. I also wrote a VOF-plic algorithm and tested that and it works. Now when I couple the two together and add gravity it doesnt work. Any suggestions on how to treat gravity ? I have modified my single phase solver to include dimensional quantities and density and rho are used explicitly. It's based on a predictor corrector step. When I couple the vof with the single phase I treat the gravity term as a constant and add it to the non-linear and viscous terms in the predictor step. Is that the way to go about it ? I'm trying to simulate the Rayleigh-Taylor problem. Your input would be highly appreciated. |
|
|
|

|
|
|
|
|
#2 |
|
Member
Join Date: Jul 2011
Posts: 59
Rep Power: 15  |
It would help to know what exactly isn't working. Using the current values of density and viscosity for create an explicit time stepping method should be ok. Not sure what you mean by treating the gravity term as a constant though.
Also you can incorporate gravity as a boundary condition at the interface instead of body force that acts throughout your whole domain. |
|
|
|

|
|
|
|
|
#3 | |
|
New Member
Kareem
Join Date: Mar 2012
Posts: 9
Rep Power: 14  |
Quote:
u*-u = dt * ( nonlin_terms + visc terms) what I did was just add gravity to that: u*-u = dt * ( nonlin_terms + visc terms +g ) where g = -9.8 and it doesnt work. When I plot the velocity vectors I dont get vectors pointing down. Also how would you apply gravity to boundary conditions ? |
||
|
|

|
||
|
|
|
#4 |
|
Member
Join Date: Jul 2011
Posts: 59
Rep Power: 15  |
You should be including the density in your gravity term
u*-u = dt * ( nonlin_terms + visc terms +g*rho(x) ) rho(x) is the density based on the VOF in that cell You can write the stress condition at the interface as (P1 − P2)n + (  − −  ) · n = ) · n =  [ [ 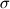 n(∇ · n) − ∇s n(∇ · n) − ∇s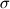 -Bo zn} -Bo zn}Bo = Bond Number and z is the elevation of the interface. |
|
|
|

|
|
|
|
|
#5 |
|
New Member
Kareem
Join Date: Mar 2012
Posts: 9
Rep Power: 14  |
I had divided my equations by rho basically solving for the non-conservative form.
For the boundary condition at the interface, does it still apply if I don't have the surface stress applied yet? From what I understand the Rayleigh-Taylor doesnt need the surface stress so can I just eliminate it from the equation you stated ? Again thanks for your prompt reply. |
|
|
|

|
|
|
|
|
#6 |
|
Member
Join Date: Jul 2011
Posts: 59
Rep Power: 15  |
Your density shouldn't be constant throughout the domain so if you are dividing out the density you should be introducing a density ratio term, rho1/rho2. then the equation would look more like
u*-u = dt * ( nonlin_terms + visc terms +g*(x)*rho(x) )/rho2 u*-u = dt * ( nonlin_terms + visc terms)/rho2 +dt*g*(x)*R where R = rho(x)/rho2 Is you interface perfectly flat, or have you introduced a perturbation to it? You should examine you pressure field to see if your getting the hydrostatic pressure correct. The boundary condition will still hold if you set the surface tension to zero and eliminate those terms. |
|
|
|

|
|
|
|
|
#7 |
|
New Member
Kareem
Join Date: Mar 2012
Posts: 9
Rep Power: 14  |
My density varies it isn't constant. Is rho2 a reference density ?
The way I do it is I say rho(x) = rho1*c + (1-c)*rho2 where c = volume fraction, rho1 = rho_liquid and rho2 = rho_gas The rho I divide by is rho(x) which is defined as above. So should I be multiplying g by rho1 or rho2 in this case ? Also my interface is perturbed. Basically for initial conditions, u = v = p = 0 I specify the perturbation by y(x) = 2+0.05*cos(2*pi*x) to give the interface that curve shape. Domain is 1x4 |
|
|
|

|
|
|
|
|
#8 |
|
Member
Ren/Xingyue
Join Date: Jan 2010
Location: Nagoya , Japan
Posts: 44
Rep Power: 16  |
That depends on the initial situations and your solver, for the boundary condition of the Poisson equation should be consist with the pressure gradient and gravity terms.
|
|
|
|

|
|
 |
|
|
 Similar Threads
Similar Threads
|
||||
| Thread | Thread Starter | Forum | Replies | Last Post |
| mass flow in is not equal to mass flow out | saii | CFX | 12 | March 19, 2018 06:21 |
| coupling vof with single phase flow and gravity term | alame005 | Main CFD Forum | 0 | August 2, 2013 15:37 |
| Two Phase Darcy flow with gravity -> problem | Cyp | OpenFOAM Programming & Development | 0 | November 17, 2010 08:58 |
| VOF gravity flow BC | Alexander Ladino | CFX | 1 | March 28, 2007 15:45 |
| Problems with the gravity in granular flow | Frank Rückert | Main CFD Forum | 0 | May 4, 2004 17:22 |